Cho hình vẽ có Ax // BC . Chứng minh AH vuông góc với BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NM
1
Những câu hỏi liên quan
B1
20 tháng 8 2017
giải thích một số từ viết tắt:tam giác(tg) , góc (g)
TH1: tia Ax và AC nằm ở 2 nửa mặt phẳng đối nhau bờ là BA. CÒn tia Ay và AB nằm 2 nwả mặt phẳng bờ đối nhau bờ là AC:
TRên tia MA lấy điểm I sao cho MI=MA. tg BAM=tg CIM(c.g.c) => g ABM=gMCI=> gACI=gACM+gBAM=180- g BAC và BA=CI
LẠi có gDAE=180-gBAC nên gACI=gDAE. Dễ dàng chứng minh được tgACI=tgEAD(c.g.c)=>DE=AI=2AM
TH2: tia Ax và AC nằm cùng phía đối với BA. Còn BA và AE cùng phía đối với AC.trên tia đối MA lấy K sao cho KM=KA
Kéo dài BC nó sẽ cắt EA ở I gEAB= gABC-gAIB=gABC-90-gACB . tg EAB=tgCAD(c.g.c)=>gEAB+gDAC
TA có : gEAD=(gEAB+gDAC)+gBAC=(gABC-90-gACB)2+(1... =gB+gC=gBCK+gACM=gACK.Chứng minh tg ACK=tgEAD(c.g.c)=>AK=ED=2AM.
29 tháng 10 2021
Cho tam giác ABC vuông góc tại B. trên cùng nửa mặt phẳng bờ chứa tia AC chứa điểm B vẽ tại tia Ax, Cy sao cho góc xAB=30 độ ,góc BCy=60 độ. Tìm kết luận
TP
21 tháng 3 2022
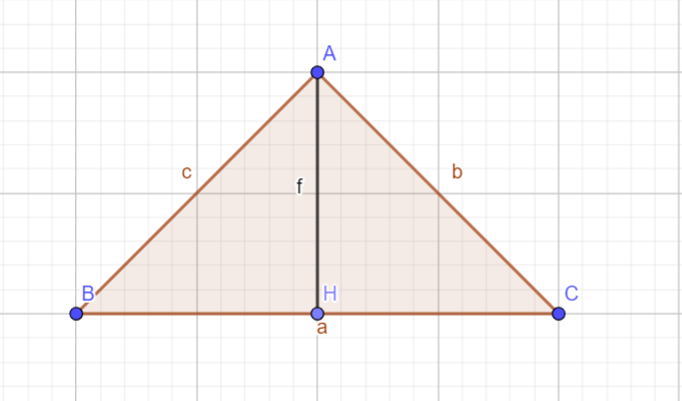
a) Xét tam giác AHB và AHC có:
AC = BC (gt)
\(\widehat{AHB}=\widehat{AHC}\) (AH vuông góc BC)
=> AHB = AHC (ch-gv)
=> HB = HC (cạnh tương ứng)
\(\widehat{BAH}=\widehat{CAH}\) (góc tương ứng)
b) Ta có HB = HC (cmt)
Mặt khác AH là cạnh góc vuông của tam giác vuông AHC
Áp dụng định lý Pitago ta có:
\(AC^2=AH^2+HC^2\\ =>10^2=AH^2+6^2\\ =>100=AH^2+36\)
\(=>AH^2=100-36=64\\ =>AH=\sqrt{64}=8\)
7 tháng 11 2021
b: Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường phân giác
6 tháng 2 2022
a) Xét tam giác AIC và tam giác BIH có:
\(\widehat{AIC}=\widehat{BIH}\)(đối đỉnh)
\(\widehat{ACI}=\widehat{BHI}=90^0\)
\(\Rightarrow\Delta AIC\sim\Delta BIH\left(g.g\right)\)
Câu b em xem lại đề nhé ! Sao AC=15cm và AC=25cm được nhỉ ?
12 tháng 3 2022
a, Xét tam giác AHB và tam giác AHC có
AH _ chung
AB = AC
Vậy tam giác AHB~ tam giác AHC (ch-cgv)
Ta có tam giác ABC cân tại A, có AH là đường cao
đồng thười là đường pg
b, Xét tam giác AMH và tam giác NAH có
HA _ chung
^MAH = ^NAH
Vậy tam giác AMH = tam giác NAH (ch-gn)
=> AM = AN ( 2 cạnh tương ứng )
c, Ta có AM/AB = AN/AC => MN // BC
d, Ta có \(AH^2+BM^2=AN^2+BH^2\)
Xét tam giác BMH vuông tại M \(MB^2=BH^2-MH^2\)
Thay vào ta được \(AH^2+BH^2-MH^2=AN^2+BH^2\Leftrightarrow AH^2-MH^2=AN^2\)
Lại có AM = AN (cmt)
\(AM^2=AH^2-MH^2\)( luôn đúng trong tam giác AMH vuông tại M)
Vậy ta có đpcm
Ta có: Ax// BC
=>\(\widehat{HAx}=\widehat{AHC}=90^0\)
=> AH _|_ BC