Cho \(\dfrac{x^2+y^2}{xy}=\dfrac{2}{3}\). Tính M= \(\dfrac{x^2+6xy+y^2}{x^2-6xy+y^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
\(A=\dfrac{x^2+y^2}{xy}+\dfrac{xy}{x^2+y^2}=\dfrac{x^2+y^2}{4xy}+\dfrac{xy}{x^2+y^2}+\dfrac{3\left(x^2+y^2\right)}{4xy}\)
\(A\ge2\sqrt{\dfrac{\left(x^2+y^2\right)xy}{4xy\left(x^2+y^2\right)}}+\dfrac{3.2xy}{4xy}=\dfrac{5}{2}\)
Dấu "=" xảy ra khi \(x=y\)
\(C=\dfrac{\left(x+y\right)^2-4xy}{xy}+\dfrac{6xy}{\left(x+y\right)^2}=\dfrac{\left(x+y\right)^2}{xy}+\dfrac{6xy}{\left(x+y\right)^2}-4\)
\(C=\dfrac{3\left(x+y\right)^2}{8xy}+\dfrac{6xy}{\left(x+y\right)^2}+\dfrac{5\left(x+y\right)^2}{8xy}-4\)
\(C\ge2\sqrt{\dfrac{18xy\left(x+y\right)^2}{8xy\left(x+y\right)^2}}+\dfrac{5.4xy}{8xy}-4=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(x=y\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 8 2021
\(C=\dfrac{\left(x+y\right)^2-4xy}{xy}+\dfrac{6xy}{\left(x+y\right)^2}=\dfrac{\left(x+y\right)^2}{xy}+\dfrac{6xy}{\left(x+y\right)^2}-4\)
\(C=\dfrac{3\left(x+y\right)^2}{8xy}+\dfrac{6xy}{\left(x+y\right)^2}+\dfrac{5\left(x+y\right)^2}{8xy}-4\)
\(C\ge2\sqrt{\dfrac{18xy\left(x+y\right)^2}{8xy\left(x+y\right)^2}}+\dfrac{5.4xy}{8xy}-4=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(x=y\)
HH
1
29 tháng 7 2021
\(\dfrac{x^2-9y^2}{x^2-6xy+9y^2}\) tại x = 1 , y = -\(\dfrac{2}{3}\)
= \(\dfrac{x^2-\left(3y\right)^2}{\left(x-3y\right)^2}\)
= \(\dfrac{\left(x-3y\right)\left(x+3y\right)}{\left(x-3y\right)}\)
= (x + 3y)
Thay x = 1 , y = -\(\dfrac{2}{3}\) vào
x + 3y
= 1 +3 . -\(\dfrac{2}{3}\)
= -1
Chúc bạn học tốt
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
Chắc đề bài là \(Q=\dfrac{3}{9x^2+6xy+y^2}+\dfrac{3}{3x^2+6xy+2y^2}\)
Từ giả thiết ta có:
\(2x^3+2xy^2+xy^2+y^3=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x\left(x^2+y^2\right)+y\left(x^2+y^2\right)=2\left(x^2+y^2\right)\)
\(\Leftrightarrow2x+y=2\)
Do đó:
\(Q=3\left(\dfrac{1}{9x^2+6xy+y^2}+\dfrac{1}{3x^2+6xy+2y^2}\right)\)
\(Q\ge\dfrac{3.4}{12x^2+12xy+3y^2}=\dfrac{4}{\left(2x+y\right)^2}=1\)
\(Q_{min}=1\) khi \(\left\{{}\begin{matrix}2x+y=2\\9x^2+6xy+y^2=3x^2+6xy+2y^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=\sqrt{6}-2\\y=6-2\sqrt{6}\end{matrix}\right.\)
TN
3 tháng 6 2017
a,\(x^2+2y^2+z^2-2xy-2y+2z+2=0\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2-2y+1\right)+\left(z^2+2x+1\right)=0\)\(\Leftrightarrow\left(x-y\right)^2+\left(y-1\right)^2+\left(z+1\right)^2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-y\right)^2=0\\\left(y-1\right)^2=0\\\left(z+1\right)^1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-y=0\\y-1=0\\z+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\y=1\\z=-1\end{matrix}\right.\)
28 tháng 7 2021
a) Ta có: \(\dfrac{3x^2-12x+12}{x^2-4}\)
\(=\dfrac{3\left(x^2-4x+4\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{3\left(x-2\right)^2}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{3\left(x-2\right)}{x+2}\)
\(=\dfrac{3\cdot\left(\dfrac{-1}{4}-2\right)}{\dfrac{-1}{4}+2}=-\dfrac{27}{7}\)
b) Ta có: \(\dfrac{x^2-5x-6}{x^2-9}\)
\(=\dfrac{\left(x-6\right)\left(x+1\right)}{\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{\left(-1-6\right)\left(-1+1\right)}{\left(-1-3\right)\left(-1+3\right)}\)
=0
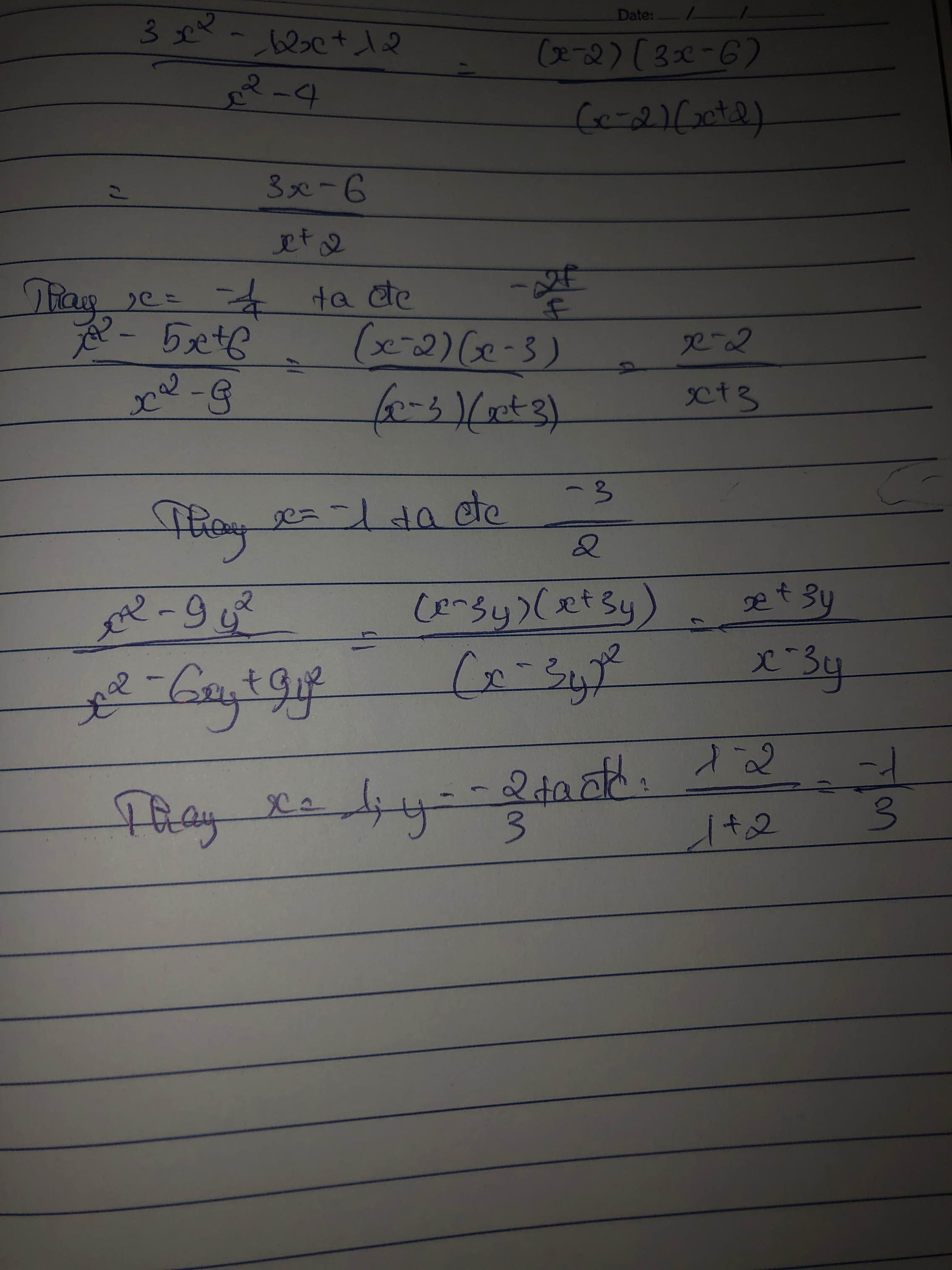
ta có: \(\dfrac{x^2+y^2}{xy}=\dfrac{2}{3}\Rightarrow2xy=3x^2+3y^2\\ \Rightarrow6xy=9x^2+9y^2\)
thay vào M, ta được:
\(M=\dfrac{x^2+9x^2+9y^2+y^2}{x^2-9x^2-9y^2+y^2}=\dfrac{10x^2+10y^2}{-8x^2-8y^2}\\ M=\dfrac{10\left(x^2+y^2\right)}{-8\left(x^2+y^2\right)}=\dfrac{10}{-8}=-\dfrac{5}{4}\)