Tìm gtln và gtnn ạ. Mình cần xem cách giải ạ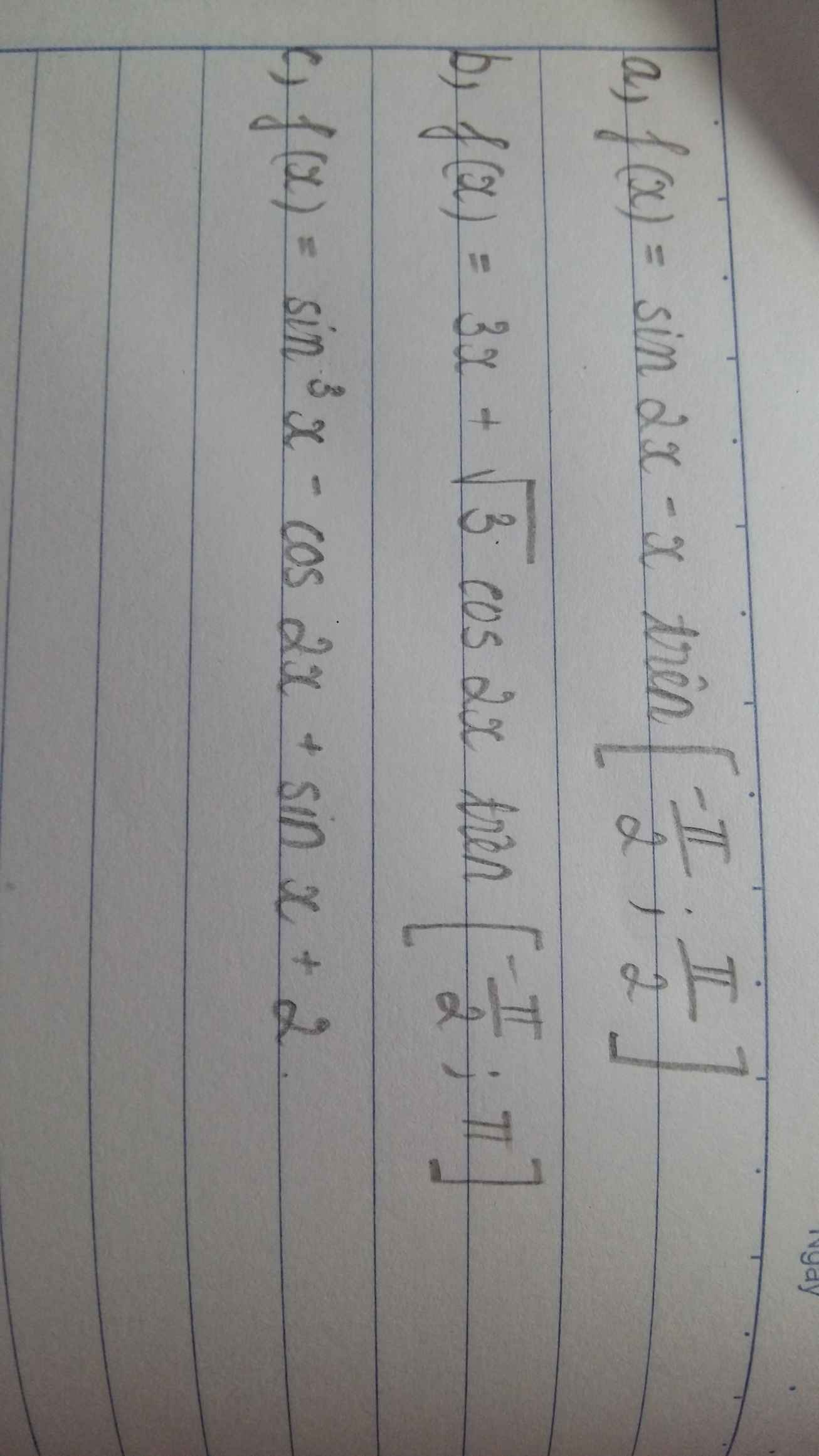
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)

Câu này em đã hỏi rồi
1.Tìm GTNN của Bthức : B= 4x2- 6x+1 : (x-2)2 với x ≠ 22. Tìm GTLN của Bthức: C= x2 + 4x - 14 : x2 -2x +1 với x≠ 1gi... - Hoc24

a) Ta có: \(M=-x^2-4x+20\)
\(=-\left(x^2+4x-20\right)\)
\(=-\left(x^2+4x+4-24\right)\)
\(=-\left(x+2\right)^2+24\le24\forall x\)
Dấu '=' xảy ra khi x=-2

Lời giải:
$K=\frac{x-2\sqrt{x-1}}{\sqrt{x}+1}=\frac{(x-1)-2\sqrt{x-1}+1}{\sqrt{x}+1}$
$=\frac{(\sqrt{x-1}-1)^2}{\sqrt{x}+1}$
Ta thấy:
$(\sqrt{x-1}-1)^2\geq 0$ với mọi $x\geq 0$
$\sqrt{x}+1>0$
$\Rightarrow K\geq 0$
Vậy $K_{\min}=0$. Giá trị này đạt tại $\sqrt{x-1}-1=0$
$\Leftrightarrow x=2$

ta có \(x\in\left[-\frac{\pi}{4};0\right]\Rightarrow2x\in\left[-\frac{\pi}{2},0\right]\Rightarrow sin2x\in\left[-1,0\right]\)
Vậy \(\hept{\begin{cases}GTNN=-1\\GTLN=0\end{cases}}\)

ĐKXĐ: \(\dfrac{3}{2}\le x\le3\)
\(A=\sqrt{2x-3}+\sqrt{6-2x}+\left(2-\sqrt{2}\right)\sqrt{3-x}\)
\(A\ge\sqrt{2x-3+6-2x}+\left(2-\sqrt{2}\right)\sqrt{3-x}\ge\sqrt{3}\)
\(A_{min}=\sqrt{3}\) khi \(3-x=0\Rightarrow x=3\)
\(A=1.\sqrt{2x-3}+\sqrt{2}.\sqrt{6-2x}\le\sqrt{\left(1+2\right)\left(2x-3+6-2x\right)}=3\)
\(A_{max}=3\) khi \(2x-3=\dfrac{6-2x}{2}\Rightarrow x=2\)

+1 còn tùy vào từng loại cần tìm nếu đơn giản là đa thức bậc 2 thì sử dụng máy tính hoặc cứ tìm thôi ;-;
+2 Vì \(m^2+3\ge3\) thì để dấu = xảy ra tức là : \(m^2+3=3\) \(\Leftrightarrow m^2=0\)
<=> m = 0 .

a/ \(A=\frac{1}{5+2\sqrt{6-x^2}}\)
Có: \(-x^2\le0\)với mọi x
=> \(6-x^2\le6\)
=> \(0\le\sqrt{6-x^2}\le\sqrt{6}\)
=> \(5\le5+2\sqrt{6-x^2}\le5+2\sqrt{6}\)
=> \(\frac{1}{5+2\sqrt{6}}\le\frac{1}{5+2\sqrt{6-x^2}}\le\frac{1}{5}\); với mọi x
=> \(\hept{\begin{cases}maxA=\frac{1}{5}\Leftrightarrow\sqrt{6-x^2}=0\Leftrightarrow x=\pm\sqrt{6}\\minA=\frac{1}{5+2\sqrt{6}}\Leftrightarrow\sqrt{6-x^2}=\sqrt{6}\Leftrightarrow x=0\end{cases}}\)
Vậy:...
b/ \(B=\sqrt{-x^2+2x+4}=\sqrt{-\left(x-1\right)^2+5}\)
Có: \(-\left(x-1\right)^2\le0\)với mọi x
=> \(-\left(x-1\right)^2+5\le5\)
=> \(0\le\sqrt{-\left(x-1\right)^2+5}\le\sqrt{5}\)
=> \(0\le B\le\sqrt{5}\)với mọi x
=> \(\hept{\begin{cases}maxB=\sqrt{5}\Leftrightarrow-\left(x-1\right)^2=0\Leftrightarrow x=1\\minB=0\Leftrightarrow\left(x-1\right)^2=5\Leftrightarrow x=\pm\sqrt{5}+1\end{cases}}\)
Vậy:...
a)Ta có:
\(0\le2\sqrt{6-x^2}\le2\sqrt{6}\)
\(\Leftrightarrow\frac{1}{5}\ge\frac{1}{5+2\sqrt{6-x^2}}\ge\frac{1}{5+2\sqrt{6}}=5-2\sqrt{6}\)
\(\Rightarrow\hept{\begin{cases}MAX\left(A\right)=\frac{1}{5}\\MIN\left(A\right)=5-2\sqrt{6}\end{cases}}\)Dấu "=" xảy ra khi \(\hept{\begin{cases}x=0\left(MIN\right)\\x=\sqrt{6}\left(MAX\right)\end{cases}}\)


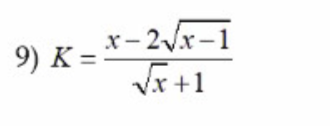

a.
\(f'\left(x\right)=2cos2x-1=0\Rightarrow cos2x=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=-\dfrac{\pi}{6}\end{matrix}\right.\)
Ta có:
\(f\left(-\dfrac{\pi}{2}\right)=0+\dfrac{\pi}{2}=\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{2}\right)=0-\dfrac{\pi}{2}=-\dfrac{\pi}{2}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\sqrt{3}}{2}-\dfrac{\pi}{6}\)
\(f\left(-\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{3}}{2}+\dfrac{\pi}{6}\)
So sánh các giá trị trên ta được:
\(f\left(x\right)_{max}=f\left(-\dfrac{\pi}{2}\right)=\dfrac{\pi}{2}\)
\(f\left(x\right)_{min}=f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}\)
b.
\(f'\left(x\right)=3-2\sqrt{3}sin2x=0\Rightarrow sin2x=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}\\x=\dfrac{\pi}{3}\end{matrix}\right.\)
Ta có: \(f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f\left(\dfrac{\pi}{6}\right)=\dfrac{\pi}{2}+\dfrac{\sqrt{3}}{2}\)
\(f\left(\dfrac{\pi}{3}\right)=\pi-\dfrac{\sqrt{3}}{2}\)
\(f\left(\pi\right)=3\pi+\sqrt{3}\)
Từ đó: \(f_{min}=f\left(-\dfrac{\pi}{2}\right)=-\dfrac{3\pi}{2}-\sqrt{3}\)
\(f_{max}=f\left(\pi\right)=3\pi+\sqrt{3}\)