Một vật giao động điều hòa theo phương trình \(x=10cos\left(2\pi t+\dfrac{\pi}{6}\right)\left(cm\right)\). Gốc thời gian đc chọn là lúc vật đi qua li độ bằng bao nhiêu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(v=x'=6pi\cdot4\cdot cos\left(6pi\cdot t+\dfrac{pi}{6}+\dfrac{pi}{2}\right)\)
\(=24pi\cdot cos\left(6pi\cdot t+\dfrac{2}{3}pi\right)\)
v'=12pi
=>cos(6pi*t+2/3pi)=1/2
=>6pi*t+2/3pi=pi/3+k2pi hoặc 6pi*t+2/3pi=-pi/3+k2pi
=>6pi*t=-1/3pi+k2pi hoặc 6pi*t=-pi+k2pi
=>t=-1/18+k/3 hoặc t=-1/6+k/3

\(T=\dfrac{2\pi}{w}=\dfrac{2\pi}{\pi}=2\left(s\right)\)
Trong 1 nửa chu kì, vật di chuyển được quãng đường là \(2\cdot10=20\left(cm\right)\)
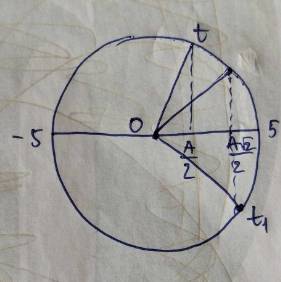
Vật khi đó phải đi từ vị trí có pha bằng \(-\dfrac{\pi}{3}\) đến vị trí có pha bằng \(\dfrac{\pi}{3}\), vì vật sẽ di chuyển được quãng đường \(\dfrac{A}{2}+\dfrac{A}{2}=A=10\left(cm\right)\)
Vậy thời gian vật phải đi là: \(\dfrac{T}{2}+\dfrac{T}{6}=\dfrac{2}{2}+\dfrac{2}{6}=\dfrac{4}{3}\left(s\right)\)

Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
Ta có: \(x=2,5\sqrt{2}=\dfrac{A\sqrt{2}}{2}\) và đang có xu hướng giảm.
Lúc này vật ở thời điểm: \(t_1=\dfrac{T}{8}\)
Tại thời điểm: \(t=\dfrac{7}{48}s=\dfrac{7T}{14}=\dfrac{T}{8}+\dfrac{T}{6}\)
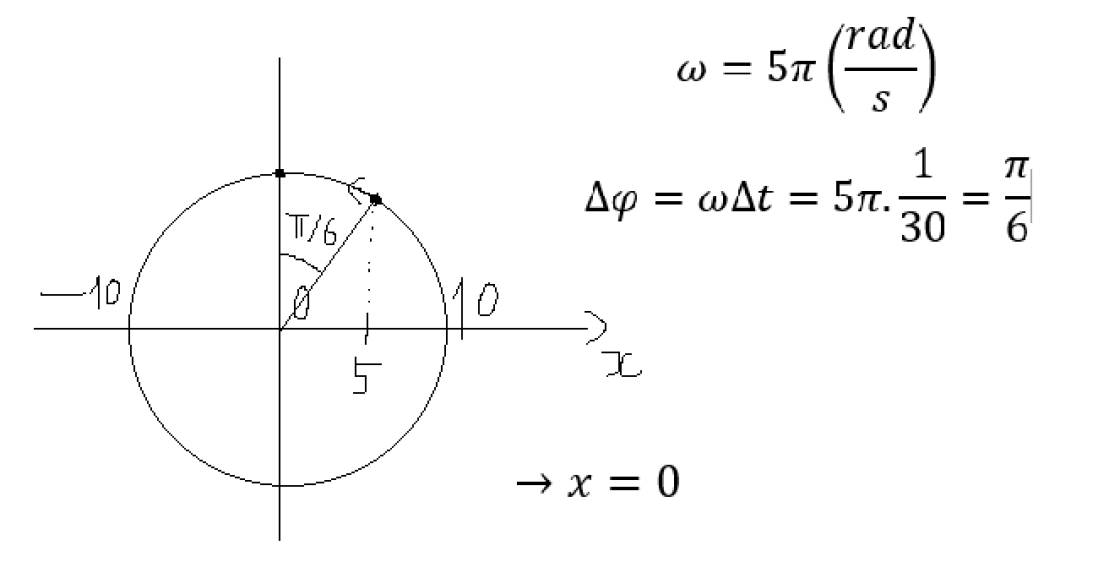
Dựa vào vòng tròn lượng giác \(\Rightarrow x=2,5cm\)

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)

Để tìm đáp án thì bạn thay t = 0 vào phương trình dao động điều hòa nhé!
Thay t = 0 vào x = 10. cos (2πt + \(\dfrac{\pi}{6}\)) ta được:
x = 10. cos (\(\dfrac{\pi}{6}\)) = 10. \(\dfrac{\sqrt{3}}{2}\) = \(\dfrac{10\sqrt{3}}{2}\) (cm)
Vậy tại gốc thời gian thì vật có li độ là x = \(\dfrac{10\sqrt{3}}{2}\) (cm)
À mà đúng rồi, bạn để ý chính tả nha, "dao động" chứ không phải là "giao động"!!!