Một vật chuyển động có phương trình đường đi là : s=16t-0,5t2
a/ Xác định chuyển động của các đặc tính này: v0 , a, tính chất chuyển động ?
b/ Viết phương trìn vận tốc và vẽ đồ thị vận tốc của vật.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 10 2021
\(S=16t-0,5t^2\) \(\Rightarrow\) v0=16m/s; a=-1m/s2
Đây là chuyển động chậm dần đều.
A
16 tháng 10 2021
a) Xét pt \(S=v_0.t+\dfrac{1}{2}a.t^2\) ta có:
\(v_0=16
\left(m\right);
a=-1
\) (m/\(s^2\))
=> Chuyển động chậm dần đều theo chiều dương TTĐ (vì a.v trái dấu)
b) Ta có: v = vo+at =16−t (m/s). Vật dừng lại khi v=0
<=> 16−t =0
<=> t =16
Vậy thời gian chuyển động của vật là t=16s
17 tháng 9 2018
a) s=16t-0,5t2 ;(m/s)
\(\Rightarrow\)\(\left\{{}\begin{matrix}v_0=16\\a=-1\end{matrix}\right.\)
tính chất chuyển động :chuyển động chậm dần đều
b) x=x0+v0.t+a.t2.0,5=16t-0,5t2
VT
8 tháng 2 2018
Chọn chiều dương là chiều chuyển động, gốc tọa độ trùng với vị trí ban đầu của vật, gốc thời gian là xuất phát.
a) Phương trình vận tốc: v = 6 + 4 t (m/s).
Đồ thị vận tốc - thời gian được biểu diễn như hình 12.
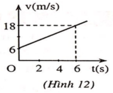
b) Khi v = 18 m/s thì t = 18 − 6 4 = 3 s.
Từ công thức v 2 − v 0 2 = 2 a s
quãng đường s = v 2 − v 0 2 2 a = 18 2 − 6 2 2.4 = 36 m.
c) Phương trình chuyển động: x = 6 t + 2 t 2 (m).
Khi v = 12 m/s thì t = 12 − 6 4 = 1 , 5 s ⇒ tọa độ x = 6.1 , 5 + 2.1 , 5 2 = 13 , 5 m.
TK
26 tháng 9 2021
ta có phương trình chuyển động của vật
\(x=-2t^2+10t+50\left(m,s\right)\Rightarrow a=-4\left(\dfrac{m}{s^2}\right);v_0=10\left(\dfrac{m}{s}\right);x_0=50\left(m\right)\)
Suy ra đây là chuyển động chậm dần đều vì a và v khác dấu
b, Phương trình vận tốc của vật
\(v=10-4t\left(\dfrac{m}{s}\right)\)
Vận tốc của vật lúc t=2s
\(v=10-4\cdot2=2\left(\dfrac{m}{s}\right)\)
c, Đường đi của vật khi vận tốc đạt được 3m/s
\(s=\dfrac{3^2-10^2}{2\cdot\left(-4\right)}=11,375\left(m\right)\)
TK
5 tháng 9 2021
a,Phương trình chuyển động của 1 vật
\(x=5+3t\left(m,s\right)\)
b,Vị trí của vật sau 4 s là:
\(x=5+3\cdot4=17\left(m\right)\)
c, <bạn tự vẽ ra nha>
7 tháng 10 2021
\(v=v_0+at\)\(=-3t+6\)
\(\Rightarrow v_0=6m\)/s và \(a=-3m\)/s2
Phương trình chuyển động của vật:
\(x=x_0+v_0t+\dfrac{1}{2}at^2=6t+\dfrac{1}{2}\cdot\left(-3\right)\cdot t^2=6t-\dfrac{3}{2}t^2\)