Cho hình thang ABCD có đáy BC=9cm AD= 30cm, cạnh bên AB=20 và CD=13. Các đường cao BH, CK chia đáy lớn AD thành các đoạn thẳng AH,HK,KD. Tính độ dài các đoạn thẳng ấy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
28 tháng 1 2021
Ta có AB//CD (2 đáy của hình thang ABCD)
\(\Rightarrow\frac{OA}{OD}=\frac{OB}{OC}=\frac{AB}{CD}\Rightarrow\frac{OA}{OA+AD}=\frac{OB}{OB+BC}=\frac{AB}{CD}\)
Từ \(\frac{OA}{OA+AD}=\frac{AB}{CD}\Rightarrow\frac{OA}{OA+9}=\frac{12}{30}\Rightarrow AO=6cm\)
Từ \(\frac{OB}{OB+BC}=\frac{AB}{CD}\Rightarrow\frac{OB}{OB+15}=\frac{12}{30}\Rightarrow OB=10cm\)

CM
12 tháng 9 2017
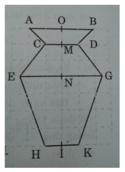
a) - Trung điểm của đoạn AB là điểm O.
- M là trung điểm của đoạn CD.
- N là trung điểm của đoạn EG.
- I là trung điểm của đoạn thẳng HK.
b) Trong các đoạn thẳng AB, CD, EG và HK:
- Đoạn thẳng có độ dài lớn nhất là EG.
- Hai đoạn thẳng có độ dài bằng nhau là CD và KH.
Ta có: BC // HK, BH // CK (cùng \(\perp\) AD)
=> \(\left\{{}\begin{matrix}BC=HK=9cm\\BH=CK=a\end{matrix}\right.\) (tính chất đoạn chắn)
Có: b + HK + c = AD
=> b + 9 + c = 30
=> b + c = 21
Áp dụng định lí Py-ta-go ta có: \(\left\{{}\begin{matrix}a^2+b^2=AB^2=20^2\\a^2+c^2=CD^2=13^2\end{matrix}\right.\)
Từ vế với vế ta được: b2 - c2 = 202 - 132
=> (b - c)(b + c) = 231
=> (b - c).21 = 231
=> b - c = 11
Mà b + c = 21 nên \(\left\{{}\begin{matrix}c=\dfrac{21-11}{2}=5=KD\\b=21-5=16=AH\end{matrix}\right.\)