cho hàm số y =f(x)=12x-2/4x+1
a tìm các giá trị nguyên của xđể f(x)là số nguyên
b tim x để f(x)lớn hơn 0 và f(x) nhỏ hơn 0
chú ý /là trên của phân số
làm nhanh hộ cái nhé
mai đi học rồi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\frac{12x-2}{4x+1}=\frac{12x+3-5}{4x+1}=3-\frac{5}{4x+1}\)
Để f(x) là số nguyên thì 5 chia hết cho (4x+1)
----------lập bảng-------
suy ra x = { 0;1}
b, *f(x)> 0
=> \(\hept{\begin{cases}12x-2>0\\4x+1>0\end{cases}}\Rightarrow\hept{\begin{cases}x>\frac{1}{6}\\x>-\frac{1}{4}\end{cases}}\Rightarrow x>\frac{1}{6}\)hoặc \(\hept{\begin{cases}12x-2< 0\\4x+1< 0\end{cases}\Rightarrow x< -\frac{1}{4}}\)
Suy ra f(x)>0 khi \(\orbr{\begin{cases}x>\frac{1}{6}\\x< -\frac{1}{4}\end{cases}}\)
*f(x)<0
=> \(\hept{\begin{cases}12x-2>0\\4x+1< 0\end{cases}\Rightarrow\hept{\begin{cases}x>\frac{1}{6}\\x< -\frac{1}{4}\end{cases}}}\)(loại)
hoặc \(\hept{\begin{cases}12x-2< 0\\4x+1>0\end{cases}\Rightarrow-\frac{1}{4}< x< \frac{1}{6}}\)
Vậy f(x) < 0 khi -1/4 <x<1/6

Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
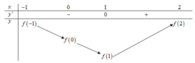
Nhận thấy
![]()
Để tìm ![]() ta so sánh f(-1) và f(2)
ta so sánh f(-1) và f(2)
Theo giả thiết, ![]()
![]()
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 ![]()
![]()

bài 1:
a) y=f(0)=|1-0|+2=3
y=f(1)=|1-(-1)|+2=4
y=f(-1/2)=|1-(-1/2)|+2=7/2
b) f(x)=3 <=> |1-x|+2=3
|1-x|=3-2
|1-x|=1
=> \(\orbr{\begin{cases}1-x=1\\1-x=-1\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
f(x)=3-x <=> |1-x|+2=3-x
|1-x|=3-x-2
|1-x|=1-x
=> (1-x)-(1-x)=0
2.(1-x)=0
=> 1-x=0
=> x=1

+ Đạo hàm f'(x) = 2 - m x 2 ( x + 1 ) x ( x + 1 )
f'(x) = 0 ⇒ x = 2 m ↔ x = m 2 4 ∈ [ 0 ; 4 ] , ∀ m > 1
+ Lập bảng biến thiên, ta kết luận được
m a x [ 0 ; 4 ] f ( x ) = f ( 4 m 2 ) = m 2 + 4
+ Vậy ta cần có m 2 + 4 < 3
↔ m < 5 → m > 1 m ∈ ( 1 ; 5 )
Chọn C.

Chọn A
Dựa vào đồ thị của hàm f'(x) ta có bảng biến thiên.
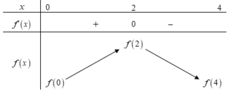
Vậy giá trị lớn nhất M = f(2)
Hàm số đồng biến trên khoảng (0;2) nên f(2) > f(1) => f(2) - f(1) > 0 .
Hàm số nghịch biến trên khoảng (2;4) nên f(2) > f(3) => f(2) - f(3) > 0.
Theo giả thuyết: f(0) + f(1) - 2f(2) = f(4) - f(3).
![]()
=> f(0) > f(4)
Vậy giá trị nhỏ nhất m = f(4)
bài này chữa r mà