Tìm tham số để phương trình sau có 2 nghiệm dương phân biệt
a) mx2 +2mx+m-2=0
b) x2 +kx+1=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 5 2022
a) Khi \(m=1\) thì pt đã cho trở thành \(x^2-2x-10=0\) (*)
pt (*) có \(\Delta'=\left(-1\right)^2-\left(-10\right)=11>0\)
Do đó (*) có 2 nghiệm phân biệt \(\left[{}\begin{matrix}x_1=\dfrac{-\left(-1\right)+\sqrt{11}}{1}=1+\sqrt{11}\\x_2=\dfrac{-\left(-1\right)-\sqrt{11}}{1}=1-\sqrt{11}\end{matrix}\right.\)
b) Xét pt đã cho \(x^2-mx-10=0\) \(\left(a=1;b=-m;c=-10\right)\)
Nhận thấy \(ac=1\left(-10\right)=-10< 0\) nên pt đã cho luôn có 2 nghiệm phân biệt \(x_1,x_2\).
Áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{-m}{1}=m\\x_1x_2=\dfrac{-10}{1}=-10\end{matrix}\right.\)
Ta có \(x_1^2+x_2^2=29\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=29\Leftrightarrow m^2-2\left(-10\right)=29\)\(\Leftrightarrow m^2+20=29\Leftrightarrow m^2=9\Leftrightarrow m=\pm3\)
Vậy để pt đã cho có 2 nghiệm phân biệt thỏa mãn đề bài thì \(m=\pm3\)
CM
14 tháng 1 2017
*Xét phương trình (m2 +1).x2 – (m- 6)x - 2= 0 có a= m2 + 1 >0 và c = -2 < 0 nên ac< 0 mọi m.
=> Phương trình (1) luôn có nghiệm mọi m.
* Phương trình x 2 + m + 3 x - 1 = 0 có ac= 1. (-1) < 0 nên phương trình này luôn có nghiệm mọi m.
* Xét (3) mx2 - 2x – m = 0 . Khi m= 0 thì (3) trở thành: - 2x = 0 đây là phương trình bậc nhất có nghiệm duy nhất là x = 0.
* Xét (4) có :
∆ = - 2 m 2 - 4 . 2 - 1 - m = 4 m 2 + 8 + 8 m = 4 m 2 + 8 m + 4 + 4 = 4 m + 1 2 + 4 > 0 ∀ m
Nên trình (4) luôn có 2 nghiệm phân biệt với mọi m.
Chọn C.
4 tháng 6 2023
a: Δ=(-2m)^2-4(2m-3)
=4m^2-8m+12
=4m^2-8m+4+8=(2m-2)^2+8>0 với mọi m
=>PT luôn có hai nghiệm pb
b: PT có hai nghiệm trái dấu
=>2m-3<0
=>m<3/2
25 tháng 1 2023
a: \(\text{Δ }=\left(-2m\right)^2-4\left(2m-5\right)=4m^2-8m+20\)
\(=4m^2-8m+4+16=\left(2m-2\right)^2+16>0\)
=>(1) luôn có hai nghiệm phân biệt
b: (x1-x2)^2=32
=>(x1+x2)^2-4x1x2=32
=>\(\left(2m\right)^2-4\left(2m-5\right)=32\)
=>4m^2-8m+20-32=0
=>4m^2-8m-12=0
=>m^2-2m-3=0
=>m=3 hoặc m=-1
AH
Akai Haruma
Giáo viên
13 tháng 3 2021
Lời giải:
PT có 2 nghiệm pb khi:
$\Delta'=m^2+m(2m+1)>0\Leftrightarrow m(3m+1)>0\Leftrightarrow m>0$ hoặc $m< \frac{-1}{3}(*)$
Theo định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=\frac{-(2m+1)}{m}\end{matrix}\right.\) . Khi đó:
$x_1^2+2x_1x_2^2+3x_2^2=4x_1+5x_2-1$
$\Leftrightarrow (x_1+x_2)^2+2x_2^2=4(x_1+x_2)+x_2-1$
$\Leftrightarrow 4+2x_2^2=7+x_2$
$\Leftrightarrow 2x_2^2-x_2-3=0$
$\Leftrightarrow x_2=\frac{3}{2}$ hoặc $x_2=-1$
$x_2=\frac{3}{2}$ thì $x_1=\frac{1}{2}$
$\frac{-(2m+1)}{m}=x_1x_2=\frac{3}{4}\Leftrightarrow m=\frac{-4}{11}$
$x_2=-1$ thì $x_1=3$
$\frac{-(2m+1)}{m}=x_1x_2=-3\Leftrightarrow m=1$
(hai giá trị trên đều thỏa mãn)
13 tháng 3 2021
Ohh em làm cách khác vẫn ra thế này! Thầy nhiệt tình thật !
17 tháng 1 2023
Bài 2:
a: TH1: m=0
=>-x+1=0
=>x=-1(nhận)
TH2: m<>0
\(\text{Δ}=\left(m-1\right)^2-4m\left(1-m\right)\)
=m^2-2m+1-4m+4m^2
=5m^2-6m+1
=(2m-1)(3m-1)
Để phương trình có nghiệm thì (2m-1)(3m-1)>=0
=>m>=1/2 hoặc m<=1/3
b: Để phương trình có hai nghiệm phân biệt thì (2m-1)(3m-1)>0
=>m>1/2 hoặc m<1/3
c: Để phương trình có hai nghiệmtrái dấu thì (1-m)*m<0
=>m(m-1)>0
=>m>1 hoặc m<0
d: Để phương trình có hai nghiệm dương phân biệt thì
\(\left\{{}\begin{matrix}m\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{1}{2};+\infty\right)\\\dfrac{-m+1}{m}>0\\\dfrac{1-m}{m}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left(-\infty;\dfrac{1}{3}\right)\cup\left(\dfrac{1}{2};+\infty\right)\\0< m< 1\end{matrix}\right.\)
=>1/2<m<1
CM
9 tháng 1 2018
Để phương trình x 2 - 2 m x + m + 2 = 0 có hai nghiệm dương phân biệt
⇔ Δ ' > 0 S > 0 P > 0 ⇔ − m 2 − 1. m + 2 > 0 2 m > 0 m + 2 > 0 ⇔ m 2 − m − 2 > 0 m > 0 m > − 2 ⇔ m < − 1 , m > 2 m > 0 m > − 2
Vậy: m > 2
Đáp án cần chọn là: A
8 tháng 3 2022
\(mx^2+\left(m-1\right)x+3-4m=0\left(1\right)\)
\(m=0\Rightarrow\)\(\left(1\right)\Leftrightarrow-x+3=0\Leftrightarrow x=3\left(ktm\right)\)
\(m\ne0\Rightarrow x1< 2< x2\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(x1-2\right)\left(x2-2\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2-4m\left(3-4m\right)>0\\x1x2-2\left(x1+x2\right)+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>\dfrac{7+4\sqrt{2}}{17}\\m< \dfrac{7-4\sqrt{2}}{17}\end{matrix}\right.\\\dfrac{3-4m}{m}-2.\left(\dfrac{1-m}{m}\right)+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>\dfrac{7+4\sqrt{2}}{17}\\m< \dfrac{7-4\sqrt{2}}{17}\end{matrix}\right.\\-\dfrac{1}{2}< m< 0\\\end{matrix}\right.\)\(\Rightarrow m\in\phi\)
CM
25 tháng 11 2018
Đáp án: B
(m - 1) x 2 - 2mx + 3m - 2 = 0 (*)
Để phương trình (*) có hai nghiệm dương phân biệt thì:
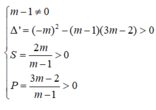
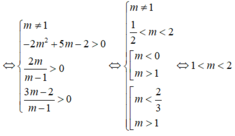
a)TH1: m=0
Phương trình trở thành : -2=0( vô lí nên loại th này)
TH2: m khác 0
Để pt có 2 nghiệm dương phương biệt thì:
\(\left\{{}\begin{matrix}\Delta>0\\\dfrac{-2m}{m}>0\\\dfrac{m-2}{m}>0\end{matrix}\right.\)(vô lý)
Vậy \(m\in\varnothing\)
b)x2+kx+1=0
Để pt có 2 nghiệm pb thì :
\(\left\{{}\begin{matrix}\Delta>0\\-k>0\\1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}k^2-4>0\\k< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}k< -2\\k>2\end{matrix}\right.\\k< 0\end{matrix}\right.\Leftrightarrow k< -2\)
Vậy k<-2