Tìm số nhỏ nhất trong các số hữu tỉ sau...
Đọc tiếp
Tìm số nhỏ nhất trong các số hữu tỉ sau :
\(\dfrac{3}{4}\);\(\dfrac{-5}{7}\);\(\dfrac{7}{-8}\);\(\dfrac{0}{5}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
3
8 tháng 4 2017
Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ
Lời giải:
Vậy những phân số biểu diễn số hữu tỉ là :
1 tháng 5 2021
Bài 1:
Ta có: \(3x=2y\)
nên \(\dfrac{x}{2}=\dfrac{y}{3}\)
mà x+y=-15
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{x+y}{2+3}=\dfrac{-15}{5}=-3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-3\\\dfrac{y}{3}=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-6\\y=-9\end{matrix}\right.\)
Vậy: (x,y)=(-6;-9)
1 tháng 5 2021
Bài 2:
a) Ta có: \(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}\)
mà x+y-z=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{3}=\dfrac{z}{5}=\dfrac{x+y-z}{4+3-5}=\dfrac{20}{2}=10\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{4}=10\\\dfrac{y}{3}=10\\\dfrac{z}{5}=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=40\\y=30\\z=50\end{matrix}\right.\)
Vậy: (x,y,z)=(40;30;50)
CM
2 tháng 3 2017
a. Số hữu tỉ âm nhỏ hơn số hữu tỉ dương. Đúng
b. Số hữu tỉ âm nhỏ hơn số tự nhiên. Đúng
c. Số 0 là số hữu tỉ dương. Sai
Vì số 0 không là số hữu tỉ dương cũng không là số hữu tỉ âm.
d. Số nguyên âm không phải là số hữu tỉ âm. Sai
Các số nguyên âm a luôn viết được dưới dạng: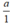 
. Do đó, số nguyên âm có là số hữu tỉ âm.
e. Tập hợp Q gồm các số hữu tỉ dương và các số hữu tỉ âm. Sai
Vì tập hợp Q gồm các số hữu tỉ dương, các số hữu tỉ âm và số 0.
8 tháng 8 2021
a: Để A là số hữu tỉ dương thì \(\dfrac{x-5}{9-x}>0\)
\(\Leftrightarrow\dfrac{x-5}{x-9}< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-5>0\\x-9< 0\end{matrix}\right.\Leftrightarrow5< x< 9\)
b: Để A không là số hữu tỉ dương cũng không là số hữu tỉ âm thì x-5=0
hay x=5
c: Để A là số nguyên thì \(x-5⋮9-x\)
\(\Leftrightarrow4⋮x-9\)
\(\Leftrightarrow x-9\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{10;8;11;7;13;5\right\}\)
NT
1
Tìm số nhỏ nhất trong các số hữu tỉ sau :
\(\dfrac{3}{4};-\dfrac{5}{7};\dfrac{-7}{8};\dfrac{0}{5}=0\)
B1 : Ta tìm BCNN(4;7;8)
+ Phân tích mỗi số ra thừa số nguyên tố : 4 = 22 ; 7 = 7 ; 8 = 23
+ Chọn ra các thừa số nguyên tố chung và riêng : 2 và 7
+ Lập tích các thừa số đã chọn . Mỗi số lấy với số mũ lớn nhất : 23 . 7 = 56
Vậy BCNN(4;7;8) = 56
B2 : Ta quy đồng các phân số để so sánh :
\(\dfrac{3}{4}=\dfrac{3.14}{4.14}=\dfrac{42}{56}\) ; \(-\dfrac{5}{7}=\dfrac{-5.8}{7.8}=-\dfrac{40}{56};-\dfrac{7}{8}=\dfrac{-7.7}{8.7}=-\dfrac{49}{56}\)
Vì \(-49< -40< 0< 42\Rightarrow-\dfrac{7}{8}< -\dfrac{5}{7}< \dfrac{0}{5}< \dfrac{3}{4}\)
Vậy số nhỏ nhất trong các số hữu tỉ \(\dfrac{3}{4};-\dfrac{5}{7};\dfrac{-7}{8};\dfrac{0}{5}=0\) là \(-\dfrac{7}{8}\)
\(-\dfrac{7}{8}\)