Giải hệ phương trình :
1. 80x + 160y = 20
2. 2x + 6y = 0,7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có : 2x+6y=0.7\(\Rightarrow\) x+3y=0.35
\(\Rightarrow\)80(x+3y)-80y=20
\(\Rightarrow\)80y=8\(\Rightarrow\) y=0.1;x=0.05
Từ phương trình (1) ta có x =(20-160y):80
thế vào phương trình (2) ta có phương trình sau 2((20-160y):80)+ 6y = 0,7
(40 -320y):80+480y:80= 0,7
80 (40-320y+480y)=0,7
40-160y=56
160y=16
y=0,1
ta có y =0,1 thế vào một trong hai phương trình suy ra x= 0,05
hoặc bạn có thể bấm máy tính bằng cách mode 5 rồi sau đó nhấn 1 rồi nhập phương trình vào máy tính, nó sẽ giải giúp bạn

\(\Leftrightarrow\left\{{}\begin{matrix}x-3y=-1\\x-3y=-1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)

\(\Leftrightarrow\left\{{}\begin{matrix}-x+3y=1\\2\left(x-3y\right)=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-3y=-1\\x-3y=-1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in R\)

ĐKXĐ: ...
Phương trình đầu tương đương:
\(2y^3+y=2\sqrt{1-x}-2x+\sqrt{1-x}\)
\(\Leftrightarrow2y^3+y=2\left(1-x\right)\sqrt{1-x}+\sqrt{1-x}\)
Đặt \(\sqrt{1-x}=a\ge0\)
\(\Rightarrow2y^3+y=2a^3+a\)
Hàm \(f\left(t\right)=2t^3+t\) có \(f'\left(t\right)=6t^2+1>0\) ;\(\forall t\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow y=a\Leftrightarrow y=\sqrt{1-x}\Rightarrow y^2=1-x\) (với \(y\ge0\))
Thế xuống pt dưới:
\(\sqrt{4x+5}=2x^2-6x-1\)
Đặt \(\sqrt{4x+5}=2t-3\Rightarrow\left\{{}\begin{matrix}2t-3=2x^2-6x-1\\4x+5=4t^2-12t+9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}t=x^2-3x+1\\x=t^2-3t+1\end{matrix}\right.\)
Hệ đối xứng, chắc tới đây bạn giải quyết được phần còn lại

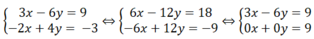
⇒ hệ phương trình vô nghiệm do phương trình 0x + 0y = 9 vô nghiệm.
Nhận xét: Hệ phương trình trên vô nghiệm.

Xét hệ phương trình 2 x − 2 y = 3 3 2 x − 6 y = 5 có 2 3 2 = − 2 − 6 ≠ 3 5 ⇔ 1 3 = 1 3 ≠ 3 5 nên hệ phương trình vô nghiệm
Đáp án: B
Ta có: \(\left\{{}\begin{matrix}80x+160y=20\\2x+6y=0,7\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}4x+8y=1\left(1\right)\\4x+12y=1,4\left(2\right)\end{matrix}\right.\)
Trừ (1) cho (2) vế theo vế ta được:
\(12y-8y=1,4-1\) <=> \(4y=0,4\)
<=> \(y=0,1\) => \(x=\dfrac{0,7-6.0,1}{2}\) = 0,05
Có 1 sự nhầm lẫn ko hề nhẹ thì phải?