Cho parabol (P) : y = x2 và đường thẳng (d) : y = 2x – m2 + 9.
Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm nằm về hai phía của trục tung.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 6 2023
Vì đường thẳng (d) cắt (P) tại hai điểm nằm về phía của trục tung nên phương trình sẽ có 2 nghiệm trái dấu
PT có 2 nghiệm trái dấu thì \(\left\{{}\begin{matrix}\Delta'>0\\P< 0\end{matrix}\right.\)
PT hoành độ giao điểm giữa ( P ) và ( d ) là \(x^2-2x+m-9=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=b'^2-ac=\left(-1\right)^2-1.\left(m-9\right)>0\\P=m-9< 0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}-m+10>0\\m-9< 0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}m< 10\\m< 9\end{matrix}\right.\\ \Leftrightarrow m< 9\)
Vậy m < 9 thì đường thẳng (d) cắt (P) tại hai điểm nằm về phía của trục tung
CM
25 tháng 9 2017
b) (d) cắt (P) tại 2 điểm A, B phân biệt nằm về 2 phía của trục tung khi và chỉ khi
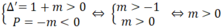
Khi đó 2 nghiệm của phương trình là:
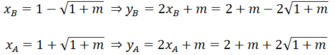
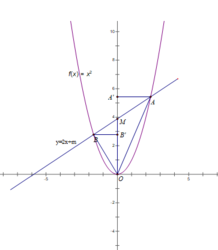
Kẻ BB' ⊥ OM ; AA' ⊥ OM
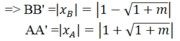
Ta có:
S A O M = 1/2 AA'.OM ; S B O M = 1/2 BB'.OM
Theo bài ra:
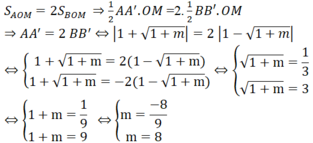
Do m > 0 nên m = 8
Vậy với m = 8 thì thỏa mãn điều kiện đề bài.
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
Pt hoành độ giao điểm:
\(x^2=2x+m\Leftrightarrow x^2-2x-m=0\) (1)
(d) cắt (P) tại 2 điểm nằm về 2 phía trục tung khi và chỉ khi (1) có 2 nghiệm trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow-m< 0\Rightarrow m>0\)
18 tháng 6 2023
PTHĐGĐ là:
x^2-2x+m-3=0
Để (P) cắt (d) hai điểm phân biệt nằm về hai phía của trục tung thì m-3<0
=>m<3
CM
20 tháng 11 2017
Phương trình hoành độ giao điểm của d và (P): x 2 = (m + 2)x – m – 1
↔ x 2 − (m + 2)x + m + 1 = 0 (1)
(d) cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung khi và chỉ khi phương trình (1) có hai nghiệm phân biệt trái dấu ↔ ac < 0 ↔ m + 1 < 0
↔ m < −1
Vậy m < −1
Đáp án: A
14 tháng 7 2023
PTHĐGĐ là:
x^2-(2m+1)x+m^2+m=0
Để (d) cắt (P) tại hai điểm phân biệt nằm về hai phía trục tung thì m^2+m<0
=>-1<m<0
AH
Akai Haruma
Giáo viên
29 tháng 3 2020
Lời giải:
1. PT hoành độ giao điểm:
$x^2-(2x-m^2+9)=0\Leftrightarrow x^2-2x+m^2-9=0(*)$
Khi $m=1$ thì pt trên trở thành: $x^2-2x-8=0$
$\Leftrightarrow (x-4)(x+2)=0\Rightarrow x=4$ hoặc $x=-2$
Khi $x=4\Rightarrow y=x^2=16$. Giao điểm thứ nhất là $(4,16)$
Khi $x=-2\Rightarrow y=x^2=4$. Giao điểm thứ hai là $(-2,4)$
2. $(P)$ và $(d)$ cắt nhau tại 2 điểm phân biệt $\Leftrightarrow (*)$ có 2 nghiệm phân biệt (hai nghiệm ấy chính là giá trị của 2 hoành độ giao điểm)
$\Leftrightarrow \Delta'=1-(m^2-9)>0\Leftrightarrow 10>m^2(1)$
Hai giao điểm nằm về phía của trục tung, nghĩa là 2 hoành độ giao điểm $x_1,x_2$ trái dấu. Điều này xảy ra khi $x_1x_2< 0\Leftrightarrow m^2-9< 0(2)$
Từ $(1);(2)$ suy ra $m^2-9< 0\Leftrightarrow -3< m< 3$
Giải:
Phương trình hoành độ điểm chung của (d) và (P) là:
\(x^2-2x+m^2-9=0\left(1\right)\)
Để (d) cắt (P) tại hai điểm phân biệt nằm về hai phía của trục tung thì phương trình (1) có hai nghiệm trái dấu.
\(\Leftrightarrow ac< 0\Leftrightarrow m^2-9< 0\)
\(\Leftrightarrow\left(m-3\right)\left(m+3\right)< 0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m-3< 0\\m+3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 3\\m>-3\end{matrix}\right.\)
\(\Leftrightarrow-3< m< 3.\) Vậy....
ta có pt hoành độ giao điểm
\(x^2=2x-m^2+9\)
\(\Leftrightarrow x^2-2x+m^2-9=0\)
ta có \(\Delta'=10-m^2\)
để pt có 2 no phân biệt thì \(\Delta'>0\)
hay \(10-m^2>0\Rightarrow-\sqrt{10}< x< \sqrt{10}\)
theo vi-ét ta có
\(\left\{{}\begin{matrix}x_1x_2=m^2-9\\x_1+x_2=2\end{matrix}\right.\)
để thỏa điều kiện thì \(x_1;x_2\) cùng dương
vậy \(x_1x_2\ge0\Leftrightarrow m^2-9\ge0\Leftrightarrow\left[{}\begin{matrix}x\le-3\\x\ge3\end{matrix}\right.\)
kết hợp điều kiện ta suy ra
để thỏa điều kiện thì \(\left[{}\begin{matrix}-\sqrt{10}< x\le-3\\3\le x< \sqrt{10}\end{matrix}\right.\)