Các bạn giải giúp mình bài 1 câu b. Và bài 2 câu b với ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
5
Những câu hỏi liên quan
13 tháng 3 2020
Bài 1
a, . Các biến đổi bất thường về cây cỏ, sâu bọ, chim chóc, loài vật... là những hiện tượng, qua đó nhân dân lao động đã đúc rút được nhiều câu tục ngữ có giá trị thực tiễn to lớn. Dự báo thời tiết của dân gian rất phong phú:
- “Trời đang nắng, cỏ gà trắng thì mưa”.
- Quạ tắm thì ráo, sáo tắm thì mưa”.
- “Gió bất hiu hiu, sếu kêu trời rét”.
- “Tháng bảy heo may, chuồn chuồn bay thì bão”.
- “Ếch kêu uôm uôm, ao chuôm đẩy nước”
- vân vân.
Ở miền Bắc nước ta, vào tháng bảy, tháng tám hàng năm thường có nhiều mưa, mưa rất to, mưa tầm tã, mưa nhiều ngày, gây ra bão, lũ lụt. Chỉ nhìn đàn kiến bò, 10 lượt kéo đi hàng đàn, nhân dân ta biết: sắp có mưa to, lũ lụt lớn sắp xảy ra: “Tháng bảy kiến bò, chỉ lo lũ lụt”. Hoặc:
- “Kiến cánh vỡ tổ bay ra, bão táp mưa sa gần tới”.
- “Kiến đen tha trứng lên cao
Thế nào cũng có mưa rào rất to”
b, “Nhất thì, nhì thục” là câu tục ngữ nêu lên kinh nghiệm về kĩ thuật trồng trọt, làm lúa nước. Thứ nhất là phải coi trọng thời vụ: “nhất thì” (kịp thời vụ, đúng thời vụ). Trái thời vụ, thời tiết là thất bát. mất án. Thứ nhì là phải cày sâu cuốc bẫm, vun xới, chăm bón, làm cỏ, không để ruộng đất hoang hóa, bạc màu; làm cho đất đai ngày một thêm màu mỡ: “nhì thục”. Yếu tố thời gian, mùa vụ, yếu tố sức lao động cần cù của con người là hai yếu tố tạo nên mùa màng tốt tươi, năng suất cao, bội thu.
c,
3 tháng 9 2021
a) \(A=\sqrt{1-x}+\sqrt{1+x}\)
\(\Rightarrow A^2=1-x+1+x+2\sqrt{\left(1-x\right)\left(1+x\right)}=2+2\sqrt{1-x^2}\)
Do \(-x^2\le0\Rightarrow1-x^2\le1\Rightarrow A^2=2+2\sqrt{1-x^2}\le2+2=4\)
\(\Rightarrow A\le2\)
\(maxA=2\Leftrightarrow x=0\)
Áp dụng bất đẳng thức: \(\sqrt{x}+\sqrt{y}\ge\sqrt{x+y}\)(với \(x,y\ge0\))
\(\Leftrightarrow\left(\sqrt{x}+\sqrt{y}\right)^2\ge x+y\)
\(\Leftrightarrow x+y+2\sqrt{xy}\ge x+y\Leftrightarrow2\sqrt{xy}\ge0\left(đúng\right)\)
\(A=\sqrt{1-x}+\sqrt{1+x}\ge\sqrt{1-x+1+x}=\sqrt{2}\)
\(maxA=\sqrt{2}\Leftrightarrow\)\(\left[{}\begin{matrix}1-x=0\\1+x=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
VT
2
23 tháng 10 2021
\(b,N=\left(2x-1\right)^2-4\ge-4\\ N_{min}=-4\Leftrightarrow x=\dfrac{1}{2}\\ c,P=\left(2x-5\right)^2+6\left(2x-5\right)+9-4\\ P=\left(2x-5+3\right)^2-4=\left(2x-2\right)^2-4\ge-4\\ P_{min}=-4\Leftrightarrow x=1\\ d,Q=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1\\ Q=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\\ Q_{min}=1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
AH
Akai Haruma
Giáo viên
23 tháng 10 2021
6a.
$M=x^2-x+1=(x^2-x+\frac{1}{4})+\frac{3}{4}$
$=(x-\frac{1}{2})^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$ khi $x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}$
CF
20 tháng 3 2022
Từ xưa đến nay, ý chí và nghị lực luôn là một phẩm chất cao quý cần có của mỗi người trong cuộc sống. Nói về ý chí nghị lực nhân dân ta có câu tục ngữ: “Có chí thì nên”. Câu tục ngữ đã đề cao ý chí, nghị lực trong cuộc sống và khuyên nhủ chúng ta sống cần phải có ý chí và nghị lực. Vậy chúng ta hãy cùng tìm hiểu về câu tục ngữ này.
Đầu tiên chúng ta cần hiểu chí ở đây nghĩa là gì? “Chí” chính là nghị lực, ý chí của mỗi con người, nó giúp cho con người có thể vượt qua những khó khăn thử thách để tiến tới đích, tiến tới thành công. Từ thời xưa, ý chí nghị lực đã được tìm thấy trong mỗi người Việt. Trong bao cuộc chiến tranh chống xâm lược thực dân, tinh thần, ý chí, nghị lực của nhân dân ta được phát huy cao độ.
Với những cuộc xâm lược của những đế quốc hùng mạnh như Pháp, Mĩ, chúng ta đứng trước một tình thế vô cùng nguy cấp. Song với ý chí nghị lực vượt khó nhân dân ta đã cùng đồng lòng đứng lên chống giặc ngoại xâm. Dù phải chịu rất nhiều gian khổ thậm chí là hi sinh nhưng nhân dân ta vẫn không hề lùi bước. Chúng ta đã chiến thắng và đánh đuổi được thực dân Pháp, đế quốc Mỹ ra khỏi đất nước, mang lại hòa bình cho dân tộc ta. Chiến thắng đó chính là chiến thắng của ý chí, nghị lực.
KT
Mn giúp có thể giúp mình câu C bài 4 và bài 5 được ko ạ, giải chi tiết 1 chút với ạ. Mình cảm ơn
1
14 tháng 10 2021
Bài 4:
b: Xét ΔABK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)
TM
6 tháng 4 2023
Bài III.2b.
Phương trình hoành độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\) : \(x^2=\left(m+1\right)x-m-4\)
hay : \(x^2-\left(m+1\right)x+m+4=0\left(I\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm nên phương trình \(\left(I\right)\) sẽ có hai nghiệm phân biệt. Do đó, phương trình \(\left(I\right)\) phải có :
\(\Delta=b^2-4ac=\left[-\left(m+1\right)\right]^2-4.1.\left(m+4\right)\)
\(=m^2+2m+1-4m-16\)
\(=m^2-2m-15>0\).
\(\Rightarrow m< -3\) hoặc \(m>5\).
Theo đề bài : \(\sqrt{x_1}+\sqrt{x_2}=2\sqrt{3}\)
\(\Rightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=\left(2\sqrt{3}\right)^2=12\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=12\left(II\right)\)
Do phương trình \(\left(I\right)\) có hai nghiệm khi \(m< -3\) hoặc \(m>5\) nên theo định lí Vi-ét, ta có : \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=-\dfrac{-\left(m+1\right)}{1}=m+1\\x_1x_2=\dfrac{c}{a}=\dfrac{m+4}{1}=m+4\end{matrix}\right.\).
Thay vào \(\left(II\right)\) ta được : \(m+1+2\sqrt{m+4}=12\)
Đặt \(t=\sqrt{m+4}\left(t\ge0\right)\), viết lại phương trình trên thành : \(t^2-3+2t=12\)
\(\Leftrightarrow t^2+2t-15=0\left(III\right)\).
Phương trình \(\left(III\right)\) có : \(\Delta'=b'^2-ac=1^2-1.\left(-15\right)=16>0\).
Suy ra, \(\left(III\right)\) có hai nghiệm phân biệt :
\(\left\{{}\begin{matrix}t_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{-1+\sqrt{16}}{1}=3\left(t/m\right)\\t_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{-1-\sqrt{16}}{1}=-5\left(ktm\right)\end{matrix}\right.\)
Suy ra được : \(\sqrt{m+4}=3\Rightarrow m=5\left(ktm\right)\).
Vậy : Không có giá trị m thỏa mãn đề bài.
TM
6 tháng 4 2023
Bài IV.b.
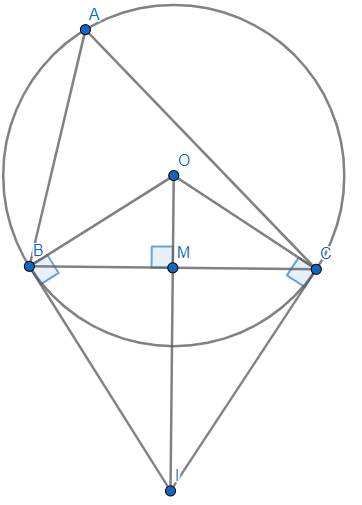
Chứng minh : Ta có : \(OB=OC=R\) nên \(O\) nằm trên đường trung trực \(d\) của \(BC\).
Theo tính chất hai tiếp tuyến cắt nhau thì \(IB=IC\), suy ra \(I\in d\).
Suy ra được \(OI\) là một phần của đường trung trực \(d\) của \(BC\) \(\Rightarrow OI\perp BC\) tại \(M\) và \(MB=MC\).
Xét \(\Delta OBI\) vuông tại \(B\) có : \(MB^2=OM.OI\).
Lại có : \(BC=MB+MC=2MB\)
\(\Rightarrow BC^2=4MB^2=4OM.OI\left(đpcm\right).\)
Tính diện tích hình quạt tròn
Ta có : \(\hat{BAC}=\dfrac{1}{2}sđ\stackrel\frown{BC}\Rightarrow sđ\stackrel\frown{BC}=2.\hat{BAC}=2.70^o=140^o\) (góc nội tiếp).
\(\Rightarrow S=\dfrac{\pi R^2n}{360}=\dfrac{\pi R^2.140^o}{360}=\dfrac{7}{18}\pi R^2\left(đvdt\right)\)
Bài 1:
a/ ĐKXĐ: \(x\ge0,x\ne1\)
\(A=\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
= \(\dfrac{15\sqrt{x}-11}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}+\dfrac{2-3\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)
= \(\dfrac{15\sqrt{x}-11+\left(\sqrt{x}+3\right)\left(2-3\sqrt{x}\right)-\left(\sqrt{x}-1\right)\left(2\sqrt{x}+3\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
= \(\dfrac{-5x+7\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
= \(\dfrac{\left(\sqrt{x}-1\right)\left(2-5\sqrt{x}\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+3\right)}\)
= \(\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}\)
b/ Với \(x\ge0,x\ne1\)
Xét hiệu \(A-\dfrac{2}{3}=\dfrac{2-5\sqrt{x}}{\sqrt{x}+3}-\dfrac{2}{3}\)
= \(\dfrac{3\left(2-5\sqrt{x}\right)-2\left(\sqrt{x}+3\right)}{3\left(\sqrt{x}+3\right)}\)
= \(\dfrac{-17\sqrt{x}}{3\left(\sqrt{x}+3\right)}\)
Ta có: \(-17\sqrt{x}\le0\) với mọi \(x\ge0\)
\(3\left(\sqrt{x}+3\right)>0\) với mọi \(x\ge0\)
\(\Rightarrow\dfrac{-17\sqrt{x}}{3\left(\sqrt{x}+3\right)}\le0\)
\(\Leftrightarrow A-\dfrac{2}{3}\le0\Leftrightarrow A\le\dfrac{2}{3}\) (đccm)
Vậy \(A\le\dfrac{2}{3}\)
Hung nguyen Ace Legona Hoang Hung Quan Xuân Tuấn Trịnh soyeon_Tiểubàng giải