A=1+4+42+43+.....+4n. .Tìm n.Biết 3A+1=425
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
15 tháng 11 2024
Olm chào em, em làm như này là cưa đúng rồi, em nhé.
L
1
8 tháng 8 2023
D=4+4^2+...+4^n
=>\(4\cdot D=4^2+4^3+...+4^{n+1}\)
=>\(3D=4^{n+1}+4^n+...+4^3+4^2-4^n-...-4^2-4\)
=>\(3D=4^{n+1}-4\)
=>\(D=\dfrac{4^{n+1}-4}{3}\)
11 tháng 11 2021
\(b,A=\left(1+4+4^2\right)+\left(4^3+4^4+4^5\right)+...\left(4^{57}+4^{58}+4^{59}\right)\\ A=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+...+4^{57}\left(1+4+4^2\right)\\ A=\left(1+4+4^2\right)\left(1+4^3+...+4^{57}\right)\\ A=21\left(1+4^3+...+4^{57}\right)⋮7\)
11 tháng 11 2021
a: \(\Leftrightarrow2x+1\in\left\{1;3\right\}\)
hay \(x\in\left\{0;1\right\}\)
16 tháng 7 2015
Lê Quang Phúc
bài 1:Tính nhanh
b)58+42+32nhân 8+5 nhân 16
c)(42 nhân 43+46nhân 57+43)-360:4
bài 2:tìm x
a)890:x=35 dư 15
c)1482:x+23=80
NK
3 tháng 8 2017
a, 21 chia hết cho 2n + 1
=> 2n + 1 thuộc Ư(21) = {1; 3; 7; 21} (do n thuộc N)
=> 2n thuộc {0; 2; 6; 20}
=> n thuộc {0; 1; 3; 10}
b, 5n + 4 chia hết cho n
Mà n chia hết cho n => 5n chia hết cho n
=> 4 chia hết cho n
=> n thuộc Ư(4) = {1; 2; 4} (do n thuộc N)
c, 3n + 7 chia hết cho n + 1
=> 3n + 3 + 4 chia hết cho n + 1
=> 3(n + 1) + 4 chia hết cho n + 1
Mà n + 1 chia hết cho n + 1 => 3(n + 1) chia hết cho n + 1
=> 4 chia hết cho n + 1
=> n + 1 thuộc Ư(4) = {1; 2; 4} (do n thuộc N)
=> n thuộc {0; 1; 3}
18 tháng 11 2018
Đặt d = (4n + 3, 5n + 1). Ta có:
\(\left\{{}\begin{matrix}4n+3⋮d\\5n+1⋮d\end{matrix}\right.\Rightarrow5\left(4n+3\right)-4\left(5n+1\right)⋮d\Rightarrow\left(20n+15\right)-\left(20n+4\right)⋮d\Rightarrow11⋮d\Rightarrow d\in\left\{1;11\right\}\)
Để hai số đó không nguyên tố cùng nhau thì d \(\ne\) 1. Do đó d = 11. Muốn d = 11 thì hai số đó đều chia hết cho 11. Ta thấy:
\(\left\{{}\begin{matrix}4n+3⋮11\Rightarrow4n+3-11⋮11\Rightarrow4n-8⋮11\Rightarrow4\left(n-2\right)⋮11\Rightarrow n-2⋮11\\5n+1⋮11\Rightarrow5n+1-11⋮11\Rightarrow5n-10⋮11\Rightarrow5\left(n-2\right)⋮11\Rightarrow n-2⋮11\end{matrix}\right.\)
Vậy, để hai số đó không nguyên tố cùng nhau thì n chia cho 11 dư 2.
18 tháng 11 2018
Cảm ơn bạn rất nhiều.Bạn học giỏi quá.Nhớ giúp mình nhiều nhé.Good bye see you later
LY
2
1 tháng 11 2023
\(A=1+4+4^2+4^3+4^4+4^5+...+4^{2019}+4^{2020}+4^{2021}\)
\(=\left(1+4+4^2\right)+\left(4^3+4^4+4^5\right)+...+\left(4^{2019}+4^{2020}+4^{2021}\right)\)
\(=21+4^3\cdot21+...+4^{2019}\cdot21\)
\(=21\left(1+4^3+...+4^{2019}\right)⋮21\)
T
1 tháng 11 2023
\(A=1+4+4^2+4^3+...+4^{2021}\\=(1+4+4^2)+(4^3+4^4+4^5)+(4^6+4^7+4^8)+...+(4^{2019}+4^{2020}+4^{2021})\\=21+4^3\cdot(1+4+4^2)+4^6\cdot(1+4+4^2)+...+4^{2019}\cdot(1+4+4^2)\\=21+4^3\cdot21+4^6\cdot21+...+4^{2019}\cdot21\\=21\cdot(1+4^3+4^6+...+4^{2019})\)
Vì \(21\cdot(1+4^3+4^6+...+4^{2019})\vdots21\)
nên \(A\vdots21\)
\(\text{#}Toru\)
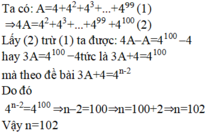
A = 1 + 4 + 42 + 43 + ... + 4n
4A = 4 + 42 + 43 + ... + 4n+1
4A - A = 4n+1 - 1
3A = 4n+1 - 1
Thay vào ta được :
4n+1 - 1 + 1 = 425
4n+1 = 425
=> n + 1 = 25
=> n = 25 - 1
=> n = 24
Vậy n = 24
baby biết copy bài anh roài à