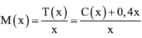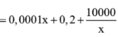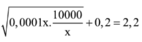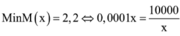chi phi san xuat ban x cuon tap chi duoc cho boi cong thuc được cho bởi 2 C= ( x ) 0, 0001x − 0, 2 x 10000 C(x) được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. 10....

AP

anh phùng quang

23 tháng 5 2017

chi phi san xuat ban x cuon tap chi duoc cho boi cong thuc được cho bởi 2 C= ( x ) 0, 0001x − 0, 2 x + 10000 C(x) được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. 10. a)Tính tổng ... a)Chứng minh rằng số tiền lãi khi in x cuốn tạp chí là 2 L( x) = −0, 0001x + 1, 8 x − 1000 b)Hỏi in bao nhiêu cuốn thì có...

Đọc tiếp

#Toán lớp 10

0

PT

Pham Trong Bach

23 tháng 5 2018

Cho phí cho xuất bản x cuốn tạp chí (bao gồm: lương cán bộ công nhan viên giấy in…) được cho bởi C ( x ) = 0 , 0001 x 2 - 0 , 2 x + 10000 , C ( x ) được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số M(x)=T(x)/x với T(x) là tổng chi phí (xuất bản và phát hành) cho x cuốn tạp chí được gọi là...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

23 tháng 5 2018

Đáp án D

Ta có

Khi đó

Suy ra

đồng

Đúng(0)

PT

Pham Trong Bach

4 tháng 8 2019

Cho phí cho xuất bản x cuốn tạp chí (bao gồm: lương cán bộ công nhan viên giấy in…) được cho bởi C x = 0 , 0001 x 2 − 0 , 2 x + 10000 , C x được tính theo đơn vị là vạn đồng. Chi phí phát hành cho mỗi cuốn là 4 nghìn đồng. Tỉ số M x = T x x với T( x) là tổng chi phí (xuất bản và phát hành) cho...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

4 tháng 8 2019

Đáp án D

Ta có

M x = T x x = C x + 0 , 4 x x = 0 , 0001 x 2 + 0 , 2 x + 10000 x = 0 , 0001 x + 0 , 2 + 10000 x

Khi đó

M x = 0 , 0001 x + 10000 x + 0 , 2 ≥ 0 , 0001 x . 10000 x + 0 , 2 = 2 , 2

Suy ra

M i n M x = 2 , 2 ⇔ 0 , 0001 x = 10000 x ⇔ x = 10000 ⇒ M x = 22.00 đ ồ n g

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

22 tháng 9 2023

Chi phí (đơn vị: nghìn đồng) để sản xuất x sản phẩm của một công ty được xác định bởi hàm số: C(x) = 50 000 + 105x.

a) Tính chi phí trung bình \(\overline C \left( x \right)\) để sản xuất một sản phẩm.

b) Tính \(\mathop {\lim }\limits_{x \to + \infty } \overline C \left( x \right)\) và cho biết ý nghĩa của kết quả.

#Toán lớp 11

1

HQ

Hà Quang Minh

Giáo viên

22 tháng 9 2023

a) \(\overline C \left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{50000 + 105x}}{x}\)

b) \(\mathop {\lim }\limits_{x \to + \infty } \overline C \left( x \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50000 + 105x}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{x\left( {\frac{{50000}}{x} + 105} \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{50000}}{x} + 105} \right) = 0 + 105 = 105\)

Vậy khi số sản phẩm càng lớn thì chi phí trung bình để sản xuất một sản phẩm tối đa 105 (nghìn đồng).

Đúng(0)

QT

Quoc Tran Anh Le

Giáo viên

23 tháng 9 2023

Tổng chi phí T (đơn vị tính: nghìn đồng) để sản xuất Q sản phẩm được cho bởi biểu thức \(T = {Q^2} + 30Q + 3300\); giá bán của 1 sản phẩm là 170 nghìn đồng. Số sản phẩm được sản xuất trong khoảng nào để đảm bảo không bị lỗ (giả thiết các sản phẩm được bán hết)?

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

23 tháng 9 2023

Doanh thu khi bán Q sản phẩm là 170Q nghìn đồng.

Lợi nhuận khi bán Q sản phẩm là \(170Q - \left( {{Q^2} + 30Q + 3300} \right)\)\( = - {Q^2} + 140Q - 3300\)(nghìn đồng)

Để không bị lỗ thì \( - {Q^2} + 140Q - 3300 \ge 0\left( 1 \right)\)

\(a = - 1 < 0;\Delta ' = 1600\)

\( - {Q^2} + 140Q - 3300 = 0\) có 2 nghiệm phân biệt \({x_1} = 30,{x_2} = 110\)

(1)\( \Leftrightarrow \)\(30 \le x \le 110\)

Vậy để không bị lỗ thì số sản phẩm được sản suất phải nằm trong khoảng từ 30 đến 110 sản phẩm.

Đúng(0)

PT

Pham Trong Bach

9 tháng 5 2018

Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí cho n máy chạy trong một giờ là 10(6n + 10) nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất? A. 4 máy B. 6 máy C. 5 máy D. 7...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

9 tháng 5 2018

Đáp án C

Giả sử có n máy thì chi phí cố định là 50n ( n = 1 ; 2 ; 3 ; . . . . ; 8 )

Để tin 50000 tờ cần 5000 3600 n = 125 9 n (giờ in)

Chi phí cho n máy chạy trong một giờ là: 10(6n + 10) nghìn đồng

Khi đó, tổng chi phí để in 50000 tờ quảng cáo là :

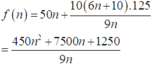
(thay 4 giá trị xem giá trị nào cho kết quả nhỏ nhất)

Lại có f(5) < f(6) nên ta sử dụng 5 máy để chi phí nhỏ nhất

Đúng(0)

PT

Pham Trong Bach

31 tháng 3 2018

Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí cho n máy chạy trong một giờ là 10(6n+10) nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy in để được lãi nhiều nhất? A.4 máy B. 6 máy. C. 5 máy. D. 7...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

31 tháng 3 2018

Chọn C.

Gọi x 0 ≤ x ≤ 8 ; x ∈ Z là số máy in sử dụng trong một giờ để được lãi nhiều nhất. Khi đó chi phí dành cho x máy in trong một giờ là 10(6x+10)=60x+100 nghìn đồng.

Chi phí vận hành 50x nghìn đồng.

Số bản in trong một giờ là 3600x suy ra thời gian để in xong 50000 tờ quảng cáo là 50000 3600 x = 125 9 x giờ

Vậy tổng chi phí là f x = 60 x + 100 25 9 x + 50 x nghìn đồng

Để lãi là nhiều nhất thì tổng chi phí là thấp nhất, vậy ta tìm giá trị nhỏ nhất của tổng chi phí.

Thay các giá trị x = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ta thấy giá trị nhỏ nhất là f 5 = 12250 9 .

Đúng(0)

PT

Pham Trong Bach

24 tháng 3 2018

Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí cho n máy chạy trong một giờ là 10 6 n + 10 nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất? A. 4 máy B. 6 máy C. 5 máy D. 7...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

24 tháng 3 2018

Đáp án C

Giả sử có n máy thì chi phí cố định là

50 n n = 1 ; 2 ; 3...8

Để in 50000 tờ cần 5000 3600. n = 125 9 n (giờ in).

Chi phí cho n máy chạy trong một giờ là 10 6 n + 10 nghìn đồng.

Khi đó, tổng chi phí để in 50000 tờ quảng cáo là:

f n = 50 n + 10 6 n + 10 .125 9 n = 450 n 2 + 7500 n + 1250 9 n

( Đến đây các em có thể thay 4 giá trị xem giá trị nào cho kết quả nhỏ nhất).

Ta có: f ' n = 0 ⇔ n = 5 3 10 ≈ 5 , 27

Lại có: f 5 < f 6 nên ta cần sử dụng 5 máy để chi phí nhỏ nhất.

Đúng(0)

PT

Pham Trong Bach

16 tháng 3 2018

Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí cho n máy chạy trong một giờ là 10 6 n + 10 nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy để được lãi nhiều nhất? A. 4 máy. B. 6 máy. C. 5 máy. D. 7...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

16 tháng 3 2018

Đáp án C

Gọi f n là hàm chi phí in 50000 tờ quảng cáo 0 < n ≤ 8 ; n ∈ ℕ . Ta cần tìm n để f(n) có giá trị thấp nhất. Theo giả thiết f(n) bao gồm chi phí vận hành cho n máy là 50n nghìn đồng. Và chi phí chạy máy sản xuất 50000 tờ quảng cáo là: 50000 3600 n 10 6 n + 10 = 2500 9 n 3 n + 5

Vậy f ( n ) = 50 n + 2500 9 n 3 n + 5 = 50 n + 250 9 n + 2500 3

Đến đây ta có thể khảo sát hàm f(n) với nnguyên để tìm chi phí thấp nhất hoặc kiểm tra trực tiếp bốn đáp án và được kết quả thấp nhất với n=5.

Đúng(0)

PT

Pham Trong Bach

15 tháng 10 2017

Một xưởng in có 8 máy in, mỗi máy in được 3600 bản in trong một giờ. Chi phí để vận hành một máy trong mỗi lần in là 50 nghìn đồng. Chi phí cho n máy chạy trong một giờ là nghìn đồng. Hỏi nếu in 50000 tờ quảng cáo thì phải sử dụng bao nhiêu máy in để được lãi nhiều nhất? A. 4 máy. B. 6 máy. C. 5 máy. D. 7...

Đọc tiếp

#Toán lớp 12

1