Cho tứ diện ABCD. Gọi P và Q lần lượt là trung điểm của các cạnh AB và CD. Trên các cạnh AC và BD ta lần lượt lấy các điểm M, N sao cho :
\(\dfrac{AM}{AC}=\dfrac{BN}{BD}=k,\left(k>0\right)\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có:
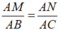
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)

Đáp án B
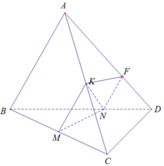
Xét (MNK) và (ABD) có:
N là điểm chung
AB // MK ⇒ A B ⫽ M N K
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua N và song song AB
d cắt AB tại điểm F cần tìm
Vì FN // AB ( cách dựng)
![]()

+) Vì I, J lần lượt là trung điểm của BD, CD nên IJ là đường trung bình của tam giác BCD. Từ đó suy ra: IJ // BC (3) .
- Từ (1) và (3) suy ra: MN // IJ .
→ Vậy tứ giác MNJI là hình thang.
+) Để MNJI là hình bình hành thì: MI// NJ.
- Lại có ba mặt phẳng (MNJI); (ABD); (ACD) đôi một cắt nhau theo các giao tuyến là MI, NJ, AD nên theo định lý 1 ta có: MI // AD // NJ (4)
- Mà I; J lần lượt là trung điểm BD,CD (5)
- Từ (4)và (5) suy ra: M, N lần lượt là trung điểm của AB, AC.
⇒ Vậy điều kiện để hình thang MNJI trở thành hình bình hành là M, N lần lượt là trung điểm của AB, AC.

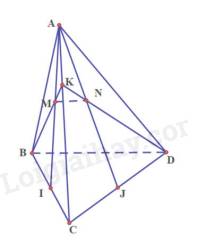
Giả sử K là trung điểm của AC
Suy ra M,N lần lượt là trọng tâm của tam giác ABC và tam giác ACD
Do đó, tam giác KBC có:\(\frac{{KM}}{{KB}} = \frac{{KN}}{{KD}} = \frac{1}{3}\)
Suy ra MN // BD
Chứng minh tương tự với trường hợp K bất kỳ

Ta sẽ áp dụng Menelaus cho 2 tam giác BCD và ABC
À quên cái dạo đầu :v
Vì lười chụp hình nên đánh máy vậy
Tìm giao điểm giữa CD và (MNQ) trước
Gán CD vô (BCD) => giao tuyến giữa (BDC) và (MNQ) là QK (K là giao điểm của MN với BC)
=> QK cắt CD tại P => (MNQ) cắt CD tại P
Rồi giờ áp dụng Menelaus cho tam giác ABC trước
\(\dfrac{AM}{MB}.\dfrac{BK}{KC}.\dfrac{CN}{NA}=1\Leftrightarrow\dfrac{1}{2}.\dfrac{BK}{KC}.1=1\Rightarrow BK=2KC\)
Áp dụng Menelaus cho tam giác BCD
\(\dfrac{BK}{KC}.\dfrac{CP}{PD}.\dfrac{DQ}{QB}=1\Leftrightarrow2.\dfrac{CP}{PD}.1=1\Rightarrow CP=\dfrac{1}{2}PD\)
\(\Rightarrow\dfrac{CP}{CD}=\dfrac{1}{3}\)

Ta có:
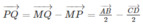
Do đó:
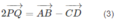
Mặt khác:
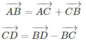
Nên
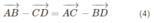
Vì 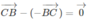
Từ (3) và (4) ta suy ra
![]()
là đẳng thức cần chứng minh.