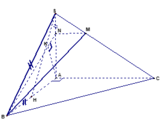
Cho tam giác ABC đều . Điểm M nằm miền trong của tam giác sao cho MA = 1cm , MC = 2cm , BM là độ dài của một cạnh hình vuông có diện tích 3cm2 . Lấy điểm D thuộc mặt phẳng bờ BC không chức điểm A sao cho tam giác CMD đều .
Chứng minh :
a) \(\Delta CAM=\Delta CBD\)
b) \(\Delta MBD\) vuông



Tự vẽ hình đi , có bài đó mà cũng phải lên đây hỏi !!!
a) Xét tam giác đều ABC có :
\(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
Xét tam giác đều MBD có :
\(\widehat{M}=\widehat{D}=\widehat{B}=60^0\)
Ta có :
\(\widehat{ACB}=\widehat{ACM}+\widehat{MCB}=60^0\)
\(\widehat{MCD}=\widehat{BCD}+\widehat{MCB}=60^0\)
=> \(\widehat{ACM}=\widehat{BCD}\)
Xét tam giác ACM và tam giác CBD có :
AC = BC (tam giác ABC đều)
CD = CM (tam giác CMD đều) => Tam giác ACM = tam giác CBD
\(\widehat{ACM}=\widehat{BCD}\)
b) Từ chứng minh tam giác trên , ta có :
BD = AM = 1cm
\(\widehat{AMC}=\widehat{BDC}\)
Xét tam giác BDM ta có :
AM = 1 = BD
BM = \(\sqrt{3}\) (Vì nó là CẠNH của một HÌNH VUÔNG có S = 3cm2)
MC = MD
Ta có :
BD2 + BM2 = 1 + 3 = 4 = MD2 = 4
=> Tam giác BMD cân tại B