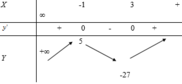
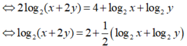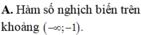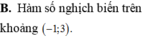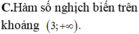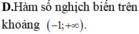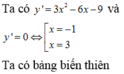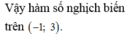cho biểu thức:M=9x^2+6y^2+18x-12xy-12y-27. Khẳng định nào sau đây là đúng?a.M > 0 b.M<0 c.M>36 d.M<36
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 12 2022
M=9x2+6y2+18x−12xy−12y−27
=(9x2−12xy+4y2)+( 18x−12y)+9+2y2−36
=[(3x)2 −2.3x.2y+(2y)2]+(18x−12y)+ 9+2y2− 36
=(3x−2y)2+2.(3x−2y) .3+32+2y2−36
=(3x−2y+3)2+2y2−36
∀x;y ta có :
(3x−2y+3)2≥0
2y2≥0
⇒(3x−2y+3)2+2y2≥0
⇒(3x-2y+3)2+2y2-36≥-36
⇒M≥-36
Dấu = xảy ra ⇔{3x−2y+3=02y2=0
⇔{x=-1 y=0
Vậy MinM=-36⇔{x=-1 y=0
Do đó : M≥−36
⇒ Chọn đáp án D
CM
17 tháng 8 2017
Chọn B.
Vì x2 + 4y2 = 12xy nên (x + 2y)2 = 16xy hay log2( x + 2y) 2= log216xy
Do đó: 2log2(x + 2y) = 4 + log2x + log2y
Vậy 
CM
31 tháng 3 2019
Đường tròn (C): x 2 + y 2 + 4 x − 6 y − 3 = 0 có tâm I(-2; 3) và bán kính R = 4.
Khoảng cách d I , ∆ = 3. − 2 − 4.3 − 2 5 = 4 nên đường thẳng tiếp xúc đường tròn.
ĐÁP ÁN B
CM
6 tháng 12 2018
Đường tròn (C): x 2 + y 2 + 8 x + 6 y + 5 = 0 có tâm I( - 4; -3) và bán kính R = 20
Khoảng cách I , ∆ = 3. − 4 − 4. − 3 − 10 5 = 2 < R nên đường thẳng cắt đường tròn tại hai điểm A, B cách nhau một khoảng là A B = 2 √ ( R 2 - ( d ( I , ∆ ) ) 2 ) = 8
ĐÁP ÁN D
