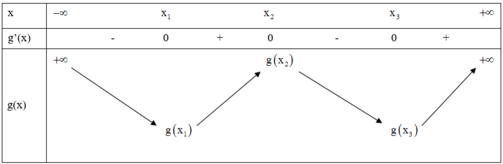
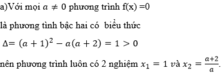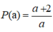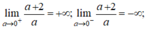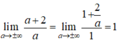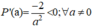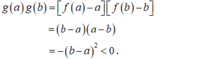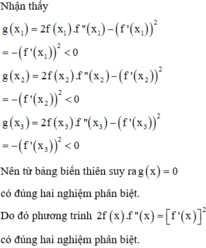Bài 1: Cho hàm số:
f(x) = ax2 – 2(a + 1)x + a + 2 ( a ≠ 0)
a) Chứng tỏ rằng phương trình f(x) = 0 luôn có nghiệm thực. Tính các nghiệm đó.
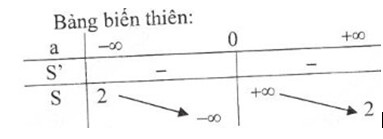
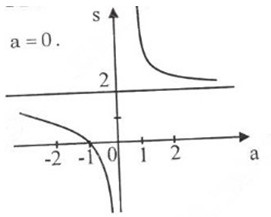
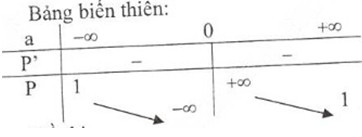
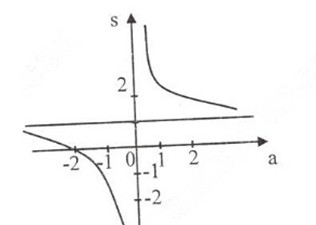
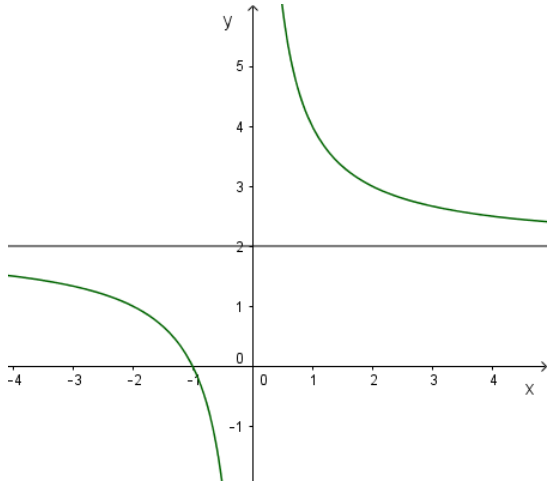
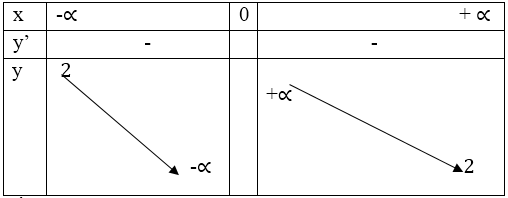
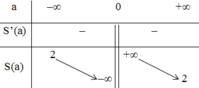
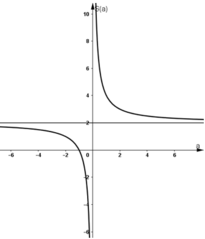
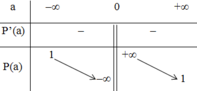
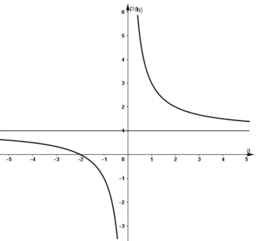
b) Tính tổng S và tích P của các nghiệm của phương trình f(x) = 0. Khảo sát sự biến thiên và vẽ đồ thị hàm số của S và P theo a.
Bài 2:
Cho hàm số: y= \(-\dfrac{1}{3}\)x3 + (a − 1)x2 + (a + 3)x − 4
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số (C) của hàm số khi a = 0
b) Tính diện tích hình phẳng giới hạn bởi (C) và đường thẳng y = 0, x = -1, x = 1
Bài 3:
Cho hàm số : y = x3 + ax2 + bx + 1
a) Tìm a và b để đồ thị của hàm số đi qua hai điểm A(1, 2) và B(-2, -1)
b) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với các giá trị tìm được của a và b.
c) Tính thể tích vật thể tròn xoay thu được khi quay hình phẳng giới hạn bởi các đường thẳng y = 0, x = 0, x = 1 và đồ thị (C) quanh trục hoành.