Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của CB lấy điểm E sao cho \(\widehat{BAD}=\widehat{CAE}\). Kẻ BH vuông góc với AD (\(H\in AD\)). Kẻ CK vuông góc với AE (\(K\in AE\))
Chứng minh :
a) BD = CE
b) BH = CK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 5 2018
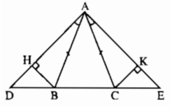
Xét tam giác BHA và ∆CKA có
∠AHB = ∠AKC = 90º
AB = AC ( vì tam giác ABC cân tại A).
∠HAB = ∠KAC ( giả thiết)
Suy ra ΔBHA = ΔCKA (cạnh huyền – góc nhọn), suy ra BH = CK.
CM
14 tháng 7 2018
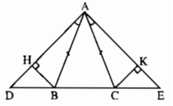
+) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)
Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)
∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)
Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE
+) Xét ΔABD và ΔACE có:
∠DAB = ∠EAC ( giả thiết)
AB = AC (vì tam giác ABC cân tại A)
∠ABD = ∠ACE ( chứng minh trên )
⇒ ΔABD = ΔACE (g.c.g)
⇒ BD = CE ( hai cạnh tương ứng)..
DT
Đỗ Thanh Hải
CTVVIP
10 tháng 3 2021
a) Do ΔABC cân tại A
=> AB = AC; góc ABC=góc ACB
Lại có: góc ABC+ góc ABD = 180o (kề bù)
góc ACB + góc ACE = 180o (kề bù)
=> góc ABD = góc ACE
Xét ΔADB và ΔAEC có:
góc BAD = góc CAE (gt)
AB = AC (cmt)
góc ABD = góc ACE (cmt)
=> ΔADB = ΔAEC (g.c.g)
=> BD = CE (2 cạnh tg ứng) đpcm
b) Vì ΔADB = ΔAEC (câu a)
=> góc ADB = góc AEC (2 góc t/ư)
hay góc HDB = góc KEC
Xét ΔBHD vuông tại H và ΔCKE vuông tại E có:
BD = CE (câu a)
góc HDB = góc KEC(cmt)
=> ΔBHD = ΔCKE (ch - gn)
=> BH = CK (2 cạnh tg ứng) (đpcm)
6 tháng 2 2022
a: Xét ΔABD và ΔACE có
\(\widehat{BAD}=\widehat{CAE}\)
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
Do đó: ΔABD=ΔACE
Suy ra: BD=CE
b: Xét ΔHDB vuông tại H và ΔKEC vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔHDB=ΔKEC
Suy ra: BH=CK
c: Ta có: ΔHDB=ΔKEC
nên \(\widehat{HBD}=\widehat{KCE}\)
mà \(\widehat{IBC}=\widehat{HBD}\)
và \(\widehat{ICB}=\widehat{KCE}\)
nên \(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>IB=IC
Xét ΔABI và ΔACI có
AB=AC
BI=CI
AI chung
DO đó: ΔABI=ΔACI
Suy ra: \(\widehat{BAI}=\widehat{CAI}\)
hay AI là tia phân giác của góc BAC
TH
2 tháng 3 2020
mình không biết vẽ hình ở đây :v
a, ΔABC cân tại A (gt) => ^ABC = ^ACB (tính chất)
^ABC + ^ABD = 180 (kề bù)
^ACB + ^ACE = 180 (kề bù)
=> ^ABD = ^ACE
xét ΔABD và ΔACE có : ^BAD = ^CAE (gt)
AB = AC vì ΔABC cân tại A (gt)
=> ΔABD = ΔACE (g-c-g)
=> BD = CE (định nghĩa)
b, xét ΔBHD và ΔCKE có : BD = CE (Câu a)
^DHB = ^EKC = 90
^ADB = ^AEC do ΔABD = ΔACE (Câu a)
=> ΔBHD = ΔCKE (ch-gn)
=> BH = CK (định nghĩa)
2 tháng 3 2020
Hình bn tự vẽ nha !!!
a) Có: \(\widehat{ABD}=180^o-\widehat{ABC};\widehat{ACE}=180^o-\widehat{ACB}\)
Mà \(\widehat{ABC}=\widehat{ACB}\)(\(\Delta\)ABC cân tại A) => \(\widehat{ABD}=\widehat{ACE}\)
Xét \(\Delta\)ABD và \(\Delta\)ACE, có:
\(\widehat{BAD}=\widehat{CAE}\)(gt) => \(\Delta\)ABD = \(\Delta\)ACE
AB = AC (\(\Delta\)ABC cân tại A) (gcg)
\(\widehat{ABD}=\widehat{ACE}\)(cmt)
=> BD = CE (2ctư)
b) Xét \(\Delta\)ABH và \(\Delta\)ACK, có:
\(\widehat{H}=\widehat{K}=90^o\)
\(AB=AC\) => \(\Delta\)ABH = \(\Delta\)ACK
\(\widehat{BAH}=\widehat{CAK}\) (CH-GN)
=> BH = CK (2ctư)
10 tháng 1 2022
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Dođó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
Suy ra: BH=CK và AH=AK
Xét ΔADE có
AH/AD=AK/AE
Do đó: HK//DE
hay HK//BC
c: Ta có: \(\widehat{OBC}=\widehat{HBD}\)
\(\widehat{OCB}=\widehat{KCE}\)
mà \(\widehat{HBD}=\widehat{KCE}\)
nên \(\widehat{OBC}=\widehat{OCB}\)
hay ΔOBC cân tại O
a) Ta có: \(\widehat{ABC}+\widehat{ABD}=180^o\) (kề bù)
\(\widehat{ACB}+\widehat{ACE}=180^o\)(kề bù)
Mà \(\widehat{ABC}=\widehat{ACB}\) (do \(\Delta ABC\) cân tại A)
Do đó: \(\widehat{ABD}=\widehat{ACE}\)
Xét hai tam giác ABD và ACE có:
\(\widehat{BAD}=\widehat{CAE}\) (gt)
AB = AC (do \(\Delta ABC\) cân tại A)
\(\widehat{ABD}=\widehat{ACE}\) (cmt)
Vậy: \(\Delta ABD=\Delta ACE\left(g-c-g\right)\)
Suy ra: BD = CE (hai cạnh tương ứng)
b) Xét hai tam giác BHD và CKE có:
BD = CE (cmt)
\(\widehat{ADB}=\widehat{AEC}\) (\(\Delta ABD=\Delta ACE\))
Vậy: \(\Delta BHD=\Delta CKE\left(ch-gn\right)\)
Suy ra: BH = CK (hai cạnh tương ứng).