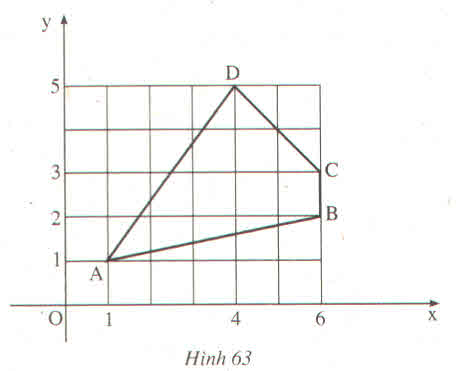
Tính độ dài các đoạn thẳng AB, BC, CD, DA trên hình 63
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có hình vẽ:
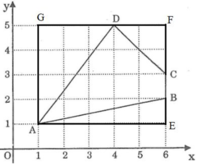
+) Áp dụng định lí py –ta-go vào tam giác ABE vuông tại E ta có:
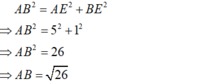
+) Áp dụng định lí py – ta- go vào tam giác DFC vuông tại F có:
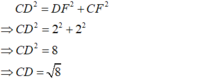
+) Áp dụng định lí Py-ta-go vào tam giác AGD vuông tại G ta có:
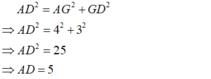
+) BC = 1

Xét ∆AHB và ∆ CKD có:HB = KD (= 1 ô)AHBˆ = CKDˆAH = CK (= 3 ô)=> ∆AHB = ∆CKD(c.g.c)=> AB = CD (cạnh tương ứng)Chứng minh tương tự ta đươc: ∆ CEB = ∆ AFD (c.g.c)suy ra BC=AD.b) Xét ∆ABD và ∆CDB có:AB = CD (cmt)BC = AD (cmt)BD chung.=> ∆ABD = ∆CDB (c.c .c)=> ABDˆ = CDBˆMà hai góc này ở vị trí so le trongVậy AB // CD (đpcm)
chả bt có khớp ko chứ lười đọc quá

Sử dụng thước kẻ đo độ dài các đoạn thẳng trong hình 46. Ta được:
AB = 12 mm, BC = 16 mm, CD = 25 mm, DA = 30 mm suy ra: AB < BC < CD < DA
Vậy thứ tự giảm dần về độ dài các đoạn thẳng là: DA, CD, BC, AB.

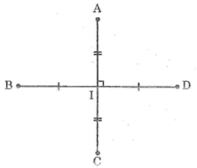
Gọi I là giao điểm của AC và BD
Ta có: I là trung điểm AC nên IA = IC = AC/2=6cm
Vì I là trung điểm của BD nên IB = ID = BD/2=8cm
Áp dụng định lí pitago vào tam giác vuông AIB ta có:
AB2=IA2+IB2
AB2=62+82=36+64=100
Vậy AB = 10 cm
Mặt khác: ΔIAB=ΔIAD=ΔICB=ΔICD(c.g.c)
Suy ra: AD = BC = CD = AB = 10cm

A C B D M
Gọi M là giao của AC và BD
Ta có: AC = 12 cm
M là trung điểm AC => AM = MC = 6 cm
Ta có: BD = 16 cm
M là trung điểm BD => BM = MD = 8 cm
Xét hai tam giác vuông ABM và CBM có:
BM: cạnh chung
AM = CM (cmt)
=> tam giác ABM = tam giác CBM (1)
Xét hai tam giác CBM và ADM có:
AM = MC (cmt)
BMC = AMD (đđ)
BM = MD (cmt)
=> tam giác CBM = tam giác ADM (2)
Xét hai tam giác vuông ADM và CDM có:
CM: chung
AM = MC (cmt)
=> tam giác ADM = tam giác CDM (3)
Từ (1);(2);(3)
=> bốn tam giác ABM; BCM; CAM; DAM bằng nhau
=> AB = BC = CD = DA
Ta có: tam giác ABM vuông
theo định lí pytago ta có:
AB2 = AM2 + BM2
=> AB2 = 62 + 82
=> AB2 = 100
=> AB = 10 cm
Có: AB = BC = CD = DA = 10 cm
Vậy: AB = 10 cm
BC = 10 cm
CD = 10 cm
DA = 10 cm.

A M B N C D
a) Trên đoạn thẳng AC ta có : AB < AC ( 5cm < 12cm )
\(\Rightarrow\)B nằm giữa A và C
\(\Rightarrow AB+BC=AC\)
\(5+BC=12\)
\(BC=12-5\)
\(BC=7\)
Vậy BC = 7cm
b) Ta có : M là trung điểm của AB
\(\Rightarrow AM=MB=\frac{AB}{2}=\frac{5}{2}=2,5\left(cm\right)\)
Ta có : N là trung điểm của BC
\(\Rightarrow BN=NC=\frac{BC}{2}=\frac{7}{2}=3,5\left(cm\right)\)
Ta có : MN = MB + BN
MN = 2,5 + 3,5
MN = 6 ( cm )
Vậy MN = 6cm
c) Ta có : CB và CD là 2 tia đối nhau
\(\Rightarrow\)C nằm giữa B và D (1)
mà BC = CD ( = 7cm ) (2)
từ (1) và (2) \(\Rightarrow\)C là trung điểm của BD
a) Có AB < AC(5cm < 12cm) nên điểm B nằm giữa hai điểm A và C
Vì điểm B nằm giữa hai điểm A và C nên ta có :
AB + BC = AC
=> 5 + BC = 12
=> BC = 7(cm)
b) Vì M là trung điểm của đoạn thẳng AB nên MB = 1/2AB = 1/2.5 = 2,5(cm)
Vì N là trung điểm của đoạn thẳng BC nên NB = 1/2BC = 1/2.7 = 3,5(cm)
=> MB + NB = 2,5 + 3,5 = 6(cm) = MN
c) Vì D là tia đối của tia CA nên điểm C nằm giữa B và D
Mà BC = CD = 7(cm) nên C là trung điểm của đoạn thẳng BD.
Ta có: \(BC=1.\)
+ Xét \(\Delta ABE\) vuông tại E có:
\(AB^2=AE^2+BE^2\) (định lí Py - ta - go).
=> \(AB^2=5^2+1^2\)
=> \(AB^2=25+1\)
=> \(AB^2=26\)
=> \(AB=\sqrt{26}\) (vì \(AB>0\)).
+ Xét \(\Delta CDF\) vuông tại F có:
\(CD^2=DF^2+CF^2\) (định lí Py - ta - go).
=> \(CD^2=2^2+2^2\)
=> \(CD^2=4+4\)
=> \(CD^2=8\)
=> \(CD=\sqrt{8}\) (vì \(CD>0\)).
+ Xét \(\Delta ADG\) vuông tại G có:
\(AD^2=AG^2+DG^2\) (định lí Py - ta - go).
=> \(AD^2=4^2+3^2\)
=> \(AD^2=16+9\)
=> \(AD^2=25\)
=> \(AD=5\) (vì \(AD>0\)).
Vậy \(AB=\sqrt{26};BC=1;CD=\sqrt{8};AD=5.\)
Chúc bạn học tốt!
Ta tính được : AB = \(\sqrt{26}\) ; CD = \(\sqrt{8}\) ; BC = 1 ; DA = 5