Cho hình 58.
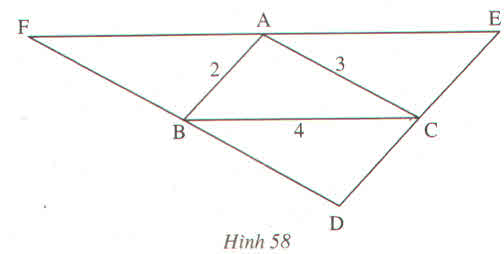
Trong đó DE // AB, DF // AC, EF // BC
Tính chu vi tam giác DEF ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
16 tháng 6 2019
Xét ΔABC và ΔABF, ta có:
∠(ABC) =∠(BAF) (so le trong)
AB cạnh chung
∠(BAC) =∠(ABF) (so le trong)
Suy ra: ΔABC= ΔBAF(g.c.g)
Suy ra: AF = BC = 4 (hai cạnh tương ứng)
BF = AC = 3(hai cạnh tương ứng)
Xét ΔABC và ΔCEA, ta có:
∠(ACB) =∠(CAE) (so le trong)
AC cạnh chung
∠(BAC) =∠(ECA) (so le trong)
Suy ra: ΔABC= ΔCEA(g.c.g)
Suy ra: AE = BC = 4(hai cạnh tương ứng)
CE = AB = 2 (hai cạnh tương ứng)
Xét ΔABC và ΔDCB, ta có:
∠(ACB) =∠(DBC) (so le trong)
BC cạnh chung
∠(ABC) =∠(DCB) (so le trong)
Suy ra: ΔABC= ΔDCB(g.c.g)
Suy ra: DC = AB = 2(hai cạnh tương ứng)
DB = AC = 3 (hai cạnh tương ứng)
Ta có: EF = AE + AF = 4 + 4=8
DF = DB + BF = 3+ 3 =6
DE = DC + CE = 2 + 2 = 4
Vậy chu vi ΔDEF là:
DE + DF + EF = 4+ 6 + 8 =18 (đơn vị độ dài)
J
8 tháng 4 2020
bài1
a) EF=??
b) không đồng dạng
c) không đồng dạng
d) Đồng dạng (vì sao thì bạn nhắn cho mình nha)
các cặp góc bằng nhau ABC=DEF; BCA=EFD; CAB=FDE
bài 2
a) theo tính chất đường trung bình trong mỗi tam giác (không hiểu thì nhắn cho mình)
ta có MN=1/2AB => MN/AB=1/2 (1)
NM=1/2BC => NP/BC=1/2 (2)
MP=1/2AC => MP/AC=1/2 (3)
từ (1),(2),(3) => MNP đồng dạng với ABC
b) vì MNP đồng dạng với ABC với tỉ số k là 2 ( theo câu a)
nên chu vi ABC = 2 lần chu vi MNP =40cm
16 tháng 3 2022
a: Xét ΔABC vuông tại A và ΔDEF vuông tại D có
AB/DE=AC/DF
Do đó: ΔABC\(\sim\)ΔDEF
b: \(\dfrac{C_{ABC}}{C_{DEF}}=\dfrac{AB}{DE}=\dfrac{2}{3}\)
2 tháng 7 2023
a: Xét ΔABC và ΔDEF có
góc A=góc D
góc B=góc E
=>ΔABC đồng dạng vơi ΔDEF
=>AB/DE=AC/DF=BC/EF
=>8/6=AC/DF=10/EF
=>EF=10*6/8=7,5cm và AC/DF=4/3
=>4DF=3AC
mà AC-DF=3
nên DF=9cm; AC=12cm
b: ΔABC đồng dạng với ΔDEF
=>S ABC/S DEF=(4/3)^2=16/9
=>S DEF=22,325625(cm2)
NV
0
21 tháng 3 2023
ΔABC đồng dạng với ΔDEF
=>AB/DE=BC/EF=AC/DF
=>7/EF=5/DF=3/6=1/2
=>EF=14cm; DF=10cm
21 tháng 3 2023
ΔABC đồng dạng với ΔDEF
=>AB/DE=BC/EF=AC/DF
=>7/EF=5/DF=3/6=1/2
=>EF=14cm; DF=10cm
KV
22 tháng 3 2023
a) Ta có:
\(\dfrac{AB}{DF}=\dfrac{6}{12}=\dfrac{1}{2}\)
\(\dfrac{AC}{EF}=\dfrac{9}{18}=\dfrac{1}{2}\)
\(\dfrac{BC}{DE}=\dfrac{12}{24}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AB}{DF}=\dfrac{AC}{EF}=\dfrac{BC}{DE}=\dfrac{1}{2}\)
Xét \(\Delta ABC\) và \(\Delta FDE\) có:
\(\dfrac{AB}{DF}=\dfrac{AC}{EF}=\dfrac{BC}{DE}\) (cmt)
\(\Rightarrow\Delta ABC\sim\Delta FDE\) (c-g-c)
Do \(\dfrac{AB}{DF}=\dfrac{AC}{EF}\) (cmt)
\(\Rightarrow AB.EF=AC.DF\)
b) Chu vi \(\Delta ABC\)
\(P_1=AB+AC+BC=6+9+12=27\left(cm\right)\)
Chu vi \(\Delta FDE\):
\(P_2=DF+EF+DE=12+18+24=54\left(cm\right)\)
Tỉ số chu vi của chúng:
\(\dfrac{P_1}{P_2}=\dfrac{27}{54}=\dfrac{1}{2}\)
KV
22 tháng 3 2023
Cách 2 (không khuyến khích làm theo cách này):
a) Ta có:
AB . EF = 6 . 18 = 108 (cm)
AC . DF = 9 . 12 = 108 (cm)
\(\Rightarrow AB.EF=AC.DF=108\left(cm\right)\)
giải
*xét tam giác abc và tam giác abf có
góc abc=góc bà(so le trong)
ad;chung
góc bac=góc abf(so le trong)
suy ra tam giác abc=tam giác abf(gcg)
suy ra af=bc=4(2 cạnh tương ứng)
bf=ac=3
*xét tam giác abc và tam giác ace có
góc acb=góc cae(số lẻ trong)
ac; chung
gốc bac= gốc eca(slt)
suy ra tam giác abc= tam giác ace
suy ra ae=bc=4(2 cạnh tương ứng)
ce=ab=2
* xét tam giác abc và tam giác dcb có
góc acb= góc dbc(slt)
bc;chung
góc abc= góc dcb
suy ra tam giác abc=tam giác dcb
suy ra dc=ab=2
db=ac=3
ta có ef=ae+af=4+4=8
df=db+bf=3+3=6
de=dc+ce=2+2=4
vậy chu vi của tam giác def là
để+DF+EF=4+6+8=18(ĐƠN VỊ ĐO ĐỘ DÀI)