Cho tam giác ABC cân tại B có \(\widehat{B}=112^0\). Kẻ đường cao AH và đường phân giác AD của tam giác đó. Tính các góc của tam giác AHD ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


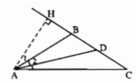
+) Ta có: ∠(ABH) + ∠(ABC) = 180º ( hai góc kề bù)
Suy ra: ∠(ABH) = 180º - ∠(ABC) = 180º − 112º = 68º
+) Xét tam giác AHB vuông tại H ta có:
∠A1+ ∠(ABH) = 90º ( tính chất tam giác vuông)
Suy ra: ∠A1= 90º − ∠(ABH) = 90º − 68º = 22º
+) Tam giác ABC cân tại B nên ∠(BAC) = ∠(ACB)
Lại có ∠(ABC) = 112º và ∠(BAC)+ ∠(ACB) + ∠(ABC) = 180º nên
∠(BAC) = (180º − 112º) : 2 = 34o
+) Do AD là tia phân giác của góc BAC nên
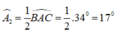
+ Từ đó
∠(HAD) = ∠A1 + ∠A2= 22º + 17º = 39º.
Tam giác HAD vuông tại H nên: ∠(HDA)+ ∠(HAD) = 90º
Suy ra: ∠(HDA) = 90º − ∠(HAD) = 90º − 39º = 51º

a) Xét ΔHBAΔHBA và ΔABCΔABC có:
ˆAHB=ˆCAB=90∘AHB^=CAB^=90∘
ˆBB^ là góc chung
⇒ΔHBA∼ΔABC⇒ΔHBA∼ΔABC (g-g)
c) ΔABCΔABC có ADAD là đường phân giác, theo tính chất đường phân giác ta có:
⇒ABAC=DBDC=1216=34⇒ABAC=DBDC=1216=34
SΔABD=12⋅AH⋅BDSΔABD=12·AH·BD
SΔACD=12⋅AH⋅DCSΔACD=12·AH·DC
⇒SΔABDSΔACD=BDDC=34⇒SΔABDSΔACD=BDDC=34


a: Xét ΔAHD vuông tại H và ΔAED vuông tại E có
AD chung
\(\widehat{HAD}=\widehat{EAD}\)
Do đó: ΔAHD=ΔAED
b: Ta có: \(\widehat{BAD}+\widehat{CAD}=90^0\)
\(\widehat{BDA}+\widehat{HAD}=90^0\)
mà \(\widehat{CAD}=\widehat{HAD}\)
nên \(\widehat{BAD}=\widehat{BDA}\)
Xét ΔABD có \(\widehat{BAD}=\widehat{BDA}\)
nên ΔBAD cân tại B
c: Xét ΔHDK vuông tại H và ΔEDC vuông tại E có
DH=DE
\(\widehat{HDK}=\widehat{EDC}\)
Do đó: ΔHDK=ΔEDC

a) xét△HBA và △ABC có:
góc BAH= góc BHA (=90 độ)
góc B chung
⇒△HBA∼△ABC (g.g)
b) áp dụng định lí pytago vào △ABC vuông tại A
AB2+AC2=BC2
⇔162+122=BC2
⇔256+144=BC2
⇔√400=20=BC(cm)
vậy BC= 20 cm
vì△HBA∼△ABC(cmt)
ta có tỉ lệ
\(\dfrac{AH}{AC}=\dfrac{AB}{BC}\)hay \(\dfrac{AH}{16}=\dfrac{12}{20}\)
⇒\(AH=\dfrac{12\cdot16}{20}=\dfrac{48}{5}=9.6\left(cm\right)\)
⇒AH = 9,6 cm
áp dụng tính chất đường phân giácAD trong tam giác
\(\dfrac{AB}{AC}=\dfrac{BD}{DC}\)⇒\(\dfrac{12}{16}=\dfrac{BD}{DC}\)⇒\(\dfrac{DC}{16}=\dfrac{BD}{12}\)
áp dụng tính chất của dãy tỉ số bằng nhau ta có
\(\dfrac{DC}{16}=\dfrac{BD}{12}=\dfrac{DC+BD}{28}=\dfrac{20}{28}=\dfrac{5}{7}\)
\(\dfrac{BD}{12}=\dfrac{5}{7}\)⇒\(BD=\dfrac{60}{7}\left(cm\right)\)
c) \(DC=BC-BD=20-\dfrac{60}{7}=\dfrac{80}{7}\)
hs tự làm![]()

a: BC=13cm
\(AB=3\sqrt{13}\left(cm\right)\)
\(AC=2\sqrt{13}\left(cm\right)\)
\(\widehat{ABH}=180^0-112^0=68^0\)
Xét ΔAHB vuông tại H có
\(\widehat{ABH}+\widehat{BAH}=90^0\)
nên \(\widehat{BAH}=22^0\)
Vì ΔABC cân tại B
nên \(\widehat{BAC}=\dfrac{180^0-112^0}{2}=34^0\)
mà AD là phân giác
nên \(\widehat{BAD}=17^0\)
=>\(\widehat{HAD}=39^0\)
hay \(\widehat{HDA}=51^0\)