giúp mik câu này vs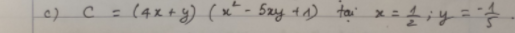 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1
Câu 1:
a: \(P=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{3x+9}{9-x}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{3x+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)-3x-9+2\sqrt{x}\cdot\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-3\sqrt{x}-3x-9+2x+6\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{3}{\sqrt{x}+3}\)
b: Thay \(x=4-2\sqrt{3}=\left(\sqrt{3}-1\right)^2\) vào Q, ta được:
\(Q=\dfrac{3}{\sqrt{\left(\sqrt{3}-1\right)^2}-1}=\dfrac{3}{\sqrt{3}-1-1}\)
\(=\dfrac{3}{\sqrt{3}-2}=-3\left(2+\sqrt{3}\right)\)
c: Đặt A=Q:P
\(=\dfrac{3}{\sqrt{x}-1}:\dfrac{3}{\sqrt{x}+3}=\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\)
Để A nguyên thì \(\sqrt{x}+3⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1+4⋮\sqrt{x}-1\)
=>\(4⋮\sqrt{x}-1\)
=>\(\sqrt{x}-1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(\sqrt{x}\in\left\{2;0;3;-1;5;-3\right\}\)
=>\(\sqrt{x}\in\left\{2;0;3;5\right\}\)
=>\(x\in\left\{0;4;9;25\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{0;4;25\right\}\)
BT
Bùi Thế Nghị
Giáo viên
22 tháng 12 2020
Giả sử X,Y được tạo từ một α-aminoaxit có CTPT CnH2n+1O2N
=>Ta xác định CTPT của Tetrapeptit X : 4CnH2n+1O2N - 3H2O <=> C4nH8n-2O5N4
Tripeptit Y : 3CnH2n+1O2N - 2H2O <=> C3nH6n-1O4N3
PT đốt cháy 0,05 mol X:
C4nH8n-2O5N4 + O2 --> 4nCO2 + (4n-1)H2O + 2N2
Từ pt cháy ta thấy nCO2 - nH2O = nX .Gọi số mol CO2,H2O thu được lần lượt là x và y ta có:
\(\left\{{}\begin{matrix}x-y=0,05\\44x+18y=36,3\end{matrix}\right.\) => \(\left\{{}\begin{matrix}x=0,6\\y=0,55\end{matrix}\right.\)
Mà \(\dfrac{nCO_2}{n_X}=4n\) => n = 3
=> Y có CTPT C9H17O4N3
Đốt cháy 0,1 mol C9H17O4N3 => 0,9 mol CO2
=> nCaCO3 = nCO2 = 0,9 <=> mCaCO3=0,9.100 = 90 gam
AM
20 tháng 2 2022
Câu 13:
Ta có: \(f\left(x\right)>0\Leftrightarrow3x-m>0\Leftrightarrow3x>m\)
Mà x>1 hay 3x>3
Vậy \(m\le3\)
Đáp án C
AM
20 tháng 2 2022
Câu 14:
(d): x-2y+1=0 hay \(\dfrac{1}{2}x+\dfrac{1}{2}=y\)
Gọi phương trình đường thẳng cần tìm là: y=ax+b
Phương trình cần tìm đi qua A nên ta có: 2=-2a+b
Để phương trình cần tìm vuông góc với (d) thì: \(a.\dfrac{1}{2}=-1\Rightarrow a=-2\)\(\Rightarrow b=-2\)
Vậy phương trình cần tìm là: \(y=-2x-2\)
Đáp án C
Ta có: \(C=\left(4x+y\right)\left(x^2-5xy+1\right)\)
\(=4x^3-20x^2y+4x-x^2y-5xy^2+y\)
\(=4x^3-21x^2y-5xy^2+4x+y\)
\(=4\cdot\dfrac{1}{8}-21\cdot\dfrac{1}{4}\cdot\dfrac{-1}{5}-5\cdot\dfrac{1}{2}\cdot\dfrac{1}{25}+4\cdot\dfrac{1}{2}+\dfrac{-1}{5}\)
\(=\dfrac{13}{4}\)
cảm ơn bn