Tam giác ABC có các đường cao BD và CE bằng nhau. Chứng minh rằng tam giác đó cân ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
6 tháng 10 2019
Xét hai tam giác vuông BDC và CEB, có:
∠(BDC) = ∠(CEB) = 90o
BD = CE (gt)
BC cạnh huyền chung
Suy ra: ΔBDC = ΔCEB
(cạnh huyền, cạnh góc vuông)
Suy ra: ∠(DCB) = ∠(EBC)
(hai góc tương ứng bằng nhau)
Hay ∠(ACB) = ∠(ABC)
Vậy ΔABC cân tại A
TT
3
27 tháng 7 2016
Xét ΔAECvà ΔADB:
GócA:chung (gt)
BD=CE(gt)
Góc D = Góc E = 90o(gt)
⇒ΔAEC=ΔADB(g.c.g)
mà ΔABCcó AB=AC(ΔAEC=ΔADB0
⇒ΔABCcân tại A.
NQ
1
15 tháng 9 2019
Xét hai tam giác vuông BDC và CEB, ta có :
\(\widehat{BDC}=\widehat{CEB}=90^o\)
\(BD=CE\left(gt\right)\)
BC cạnh huyền chung
\(\Rightarrow\Delta BDC=\Delta CEB\) (cạnh huyền, cạnh góc vuông)
\(\Rightarrow\widehat{DCB}=\widehat{EBC}\)(hai góc tương ứng bằng nhau)
Hay \(\widehat{ACB}=\widehat{ABC}\)
\(\Rightarrow\Delta ABC\) cân tại A
Vậy \(\Delta ABC\) cân tại A
Chúc bạn học tốt !!!
30 tháng 6 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
BD=CE
góc ABD=góc ACE
=>ΔADB=ΔAEC
=>AB=AC
=>ΔABC cân tại A
b: ΔABC cân tại A
mà AD là đường phân giác
nên AD vuông góc BC
Xét ΔABC có
AD,CH là đường cao
AD cắt CH tại D
=>D là trực tâm
=>BD vuông góc AC
NM
2
12 tháng 5 2023
Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
=>ΔABD=ΔACE
Sửa đề: ΔGBC cân tại G
Xét ΔEBC và ΔDCB có
EB=DC
góc EBC=góc DCB
BC chung
=>ΔEBC=ΔDCB
=>góc GBC=góc GCB
=>ΔGBC cân tại G
S
4 tháng 3 2023
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
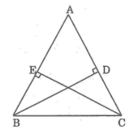
Xét hai tam giác vuông BDC và CEB:
góc BDC= góc CEB=90∘
BD = CE (gt)
BC cạnh huyền chung
Do đó: ∆BDC = ∆CEB (cạnh huyền, cạnh góc vuông)
⇒ góc DCB= góc EBC
Hay góc ACB= góc ABC
Vậy ∆ABC cân tại A.