Cho hai đường thẳng song song a, b và một cát tuyến c. Hai tia phân giác của một cặp góc trong cùng phía cắt nhau tại I. Chứng minh rằng I cách đều ba đường thẳng a, b, c.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 11 2018
Gọi A, B, C lần lượt là chân đường vuông góc kẻ từ I đến a, b, c. Xét hai góc trong cùng phía E và F. Do I thuộc tia phân giác của góc E nên IA = IC. (1)
Do I thuộc tia phân giác của góc F nên IC = IB. (2)
Từ (1) và (2) suy ra IA = IB = IC, tức là I cách đều ba đường thẳng a, b, c.
AK
7 tháng 11 2016
ta có: a//b => \(\widehat{A}+\widehat{B}=180^o\)
\(\widehat{A}_1+\widehat{B}_1=\frac{\widehat{A}}{2}+\frac{\widehat{B}}{2}=\frac{\widehat{A}+\widehat{B}}{2}=\frac{180^o}{2}=90^o\)
\(\widehat{O}=180^o-\left(\widehat{A_1}+\widehat{B_1}\right)=180^o-90^o=90^o\)
=> AO_|_BO tại O
CM
5 tháng 11 2017
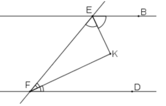
Giả sử đường thẳng AB // CD cắt đường thẳng EF tại E và F
Ta có: ∠BEF + ∠EFD = 180o (hai góc trong cùng phía)
+) Do EK là tia phân giác của góc ∠ BEF nên:
∠E1 = 1/2 .∠ (BEF) (1)
+) Do FK là tia phân giác của góc EFD nên :
∠F1 = 1/2 .∠EFD (2)
Từ (1) và (2) suy ra:
∠E1 +∠F1 =1/2 .(∠BEF + ∠EFD ) = 1/2 . 180º = 90º ( ∠BEF + ∠EFD = 180º hai góc trong cùng phía)
Trong ΔEKF,ta có:
∠EKF = 180o-(∠E1 + ∠F1) = 180o-90o=90o
Vậy EK ⊥FK
6 tháng 10 2018
giải:
giả sử đường thẳng d căt 2 đường thẳng song song tại A, B, đường phân giác góc A và B cắt nhau tại M
2 góc trong cùng phía có tổng = 180 độ
=> (MBA + MAB) = 180/2 = 90 độ
=> BMA = 180 - MAB - MBA = 180 - 90 = 90 độ
hay AM vuông góc với BM
26 tháng 10 2018
+ a // b
∠ aAb slt ∠ cBA
=> ∠ aAb = ∠ cBA (tc) (1)
+ AI là pg của ∠ aAB => ∠ A1 = ∠ aAB : 2 (2)
+ BX là pg của ∠ cBA => ∠ B1 = ∠ cBA : 2 (3)
(1)(2)(3) => ∠ A1 = ∠ B1 mà ∠ A1 slt ∠ B1
nên BX // AI
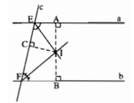
Gọi A, B, C lần lượt là chân đường vuông góc kẻ từ I đến a, b, c.
Xét hai góc trong cùng phía E và F.
Do I thuộc tia phân giác của góc E nên IA = IC(1)
Do I thuộc tia phân giác của góc F nên IC = IB(2)
Từ (1) và (2) suy ra IA = IB = IC
hay I cách đều ba đường thẳng a, b, c.