Cho tam giác nhọn ABC. Tìm điểm D thuộc trung tuyến AM sao cho d cách đều hai cạnh của góc B ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 9 2017
Vì D cách đều hai cạnh của góc B nên D nằm trên đường phân giác của ∠(ABC)
Đồng thời D nằm trên đường trung tuyến AM.
Vậy D là giao điểm của đường phân giác của ∠(ABC) và đường trung tuyến AM
CM
10 tháng 4 2018
D cách đều hai cạnh của góc B nên D nằm trên tia phân giác của góc B
Mà theo giả thiết điểm D thuộc trung tuyến AM
Do đó D là giao điểm của đường phân giác góc B với trung tuyến AM
Chọn đáp án D
ST
0
4 tháng 4 2017
Ta kẻ đường phân giác BE của góc B
Lấy D là giao điểm của BE và AM, ta có D cách đều 2 cạnh của góc B
Vậy D là giao của BE và AM
ST
0
LV
0
4 tháng 4 2023
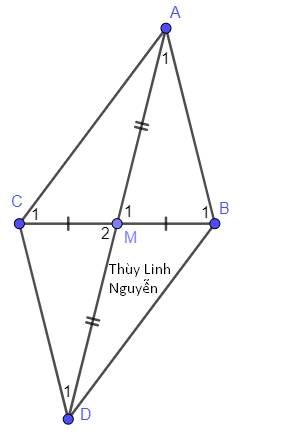
`a)`
Có `AM` là trung tuyến `=>M` là tđ `BC=>BM=CM`
Xét `Delta ABM` và `Delta DCM` có :
`{:(BM=CM(cmt)),(hat(M_1)=hat(M_2)(đối.đỉnh)),(AM=DM(Gt)):}}`
`=>Delta ABM=Delta DCM(c.g.c)(đpcm)`
`b)`
Có `Delta ABM=Delta DCM(cmt)`
`=>hat(A_1)=hat(D_1)(2` góc t/ứng `)`
mà `2` góc này ở vị trí Soletrong
nên `AB////CD(đpcm)`
`c)`
Có `AC>AB(GT)`
mà `AC` là cạnh đối diện của `hat(B_1)`
`AB` là cạnh đối diện của `hat(C_1)`
nên `hat(B_1)>hat(C_1)`(mối quan hệ góc và cạnh đối diện trong `Delta` )(đpcm)
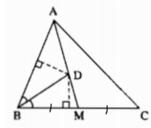
D cách đều hai cạnh của góc B nên D nằm trên đường phân giác của góc ABC
D nằm trên đường trung tuyến AM.
Vậy D là giao điểm của đường phân giác của góc ABC và đường trung tuyến AM.
Ta có hình vẽ: