cho đường tròn tâm O và điểm A nằm ngoài đường tròn đó . vẽ các tiếp tuyến AB, AC và cát tuyến ADE tới đường tròn [B và C là tiếp điểm ]. gọi H là trung điểm của DE
chứng minh
1)5 điểm A, B, H , O, C cùng thuộc một đường tròn.
2)HA là tia phân giác của góc BHC.
3)gọi I là giao điẻm của BC và DE. chứng minh : AB^2= AI . AH
4)cho BH cắt đường tròn tâm O ở K. chứng minh AE song song với CK.

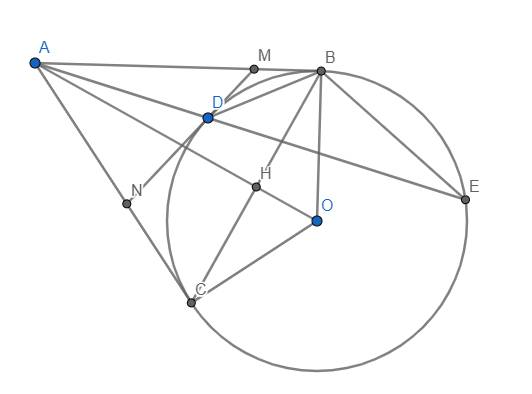


câu b: ACO=AHO mà góc ACO và góc AHO là 2 góc kề nhau => ACHO nội tiếp (tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới 1 góc ko đổi thì nội tiếp)