Cho hàm số y=(f) =x3+x2+x-5
a) giải bất phương trình :y'<=6
b) viết phương trình tiếp tuyến với đồ thị hàm số , biết tiếp tuyến có hệ số góc bằng 6
Các bạn giải nhanh dum mình
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 8 2021
\(f\left(x-3\right)+5-m>0\)
\(\Leftrightarrow\left(x-3\right)^2+5-m>0\)
\(\Leftrightarrow x^2-6x+14-m>0\)
BPT có tập nghiệm là R khi:
\(\Delta'=9-\left(14-m\right)< 0\)
\(\Leftrightarrow m< 5\)
CM
12 tháng 9 2017
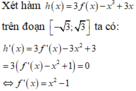
Dựng đồ thị hàm số y = x 2 - 1 cùng một hệ trục tọa độ với đồ thị hàm số y=f’(x) bài cho ta được:
16 tháng 4 2023
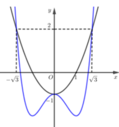
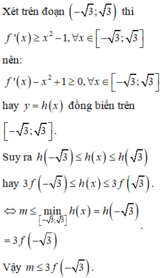
f'(x)=y'=-3x^2+2x
f'(2)=-3*2^2+2*2=-3*4+4=-8
f(2)=-2^3+2^2-1=-8-1+4=-9+4=-5
y=f(2)+f'(2)(x-2)
=-5+(-8)(x-2)
=-8x+16-5
=-8x+11
y' = 3x2 +2x +1
a. y' <= 6
<=> 3x2 + 2x +1 <=6
<=.> \(\dfrac{-5}{3}\) <= x <= 1
B. K=6
<=> 3x2 + 2x +1 = 6
<=> \(\left[{}\begin{matrix}x=1\\x=\dfrac{-5}{3}\end{matrix}\right.\)
với x= 1 => y= -2
vập pttt: y = 6 (x-1) -2
<=> y = 6x - 8
với x=\(\dfrac{-5}{3}\) => y = \(\dfrac{-230}{27}\)
vập pttt : y= 6( x + \(\dfrac{5}{3}\) ) - \(\dfrac{230}{27}\)
<=> y = 6x + \(\dfrac{40}{27}\)