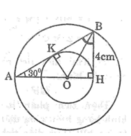
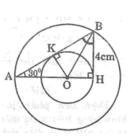
Cho tam giác AHB có \(\widehat{H}=90^0,\widehat{A}=30^0,BH=4cm\). Tia phân giác của góc B cắt AH tại O. Vẽ đường tròn (O; OH) và đường tròn (O; OA)
a) Chứng minh đường tròn (O; OH) tiếp xúc với cạnh AB
b) Tính diện tích hình vành khăn nằm giữa hai đường tròn trên