cho tam giac MNP co MH la duong trung truc dong thoi la duong cao chung minh rang:
a, tam giac MNH la tam giac can
b, MH la tia phan giac
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

GIẢI
-Xét tam giac ABC và tam giác ACM:
AMchung
M1^=M2^=90
BM=CN(gt)
=> Tam giác ABC=tam giác ACM (2 cạnh góc vuông)
=> AB=AC(cạnh tương ứng)
=>Tam giác ABC cân

Cho tam giác ABC có đường trung tuyến được vẽ từ đỉnh A vuông góc với cạnh đối diện BC tại trung điểm D của BC.
2 tam giác vuông ADB,ADC bằng nhau vì có chung cạnh góc vuông AD , 2 cạnh góc vuông còn lại là DB = DC (vì D là trung điểm của BC)
=> 2 cạnh tương ứng AB = AC hoặc 2 góc tương ứng ABD = ACD => Tam giác ABC cân tại A

Xét \(\Delta AMC\)và \(\Delta ABC\)có
Chung chiều cao hạ từ A xuống BC
\(MC=\frac{1}{4}BC\)
=>\(S_{AMC}=\frac{1}{4}S_{ABC}\)
Mặt khác \(\Delta AMC\)và \(\Delta ABC\)có chung đáy AC =>\(MH=\frac{1}{4}BK\)

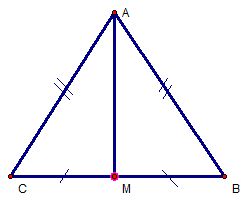
a) Xét 2 \(\Delta\) \(ABM\) và \(ACM\) có:
\(AB=AC\left(gt\right)\)
\(BM=CM\) (vì M là trung điểm của \(BC\))
Cạnh AM chung
=> \(\Delta ABM=\Delta ACM\left(c-c-c\right)\)
=> \(\widehat{BAM}=\widehat{CAM}\) (2 góc tương ứng)
=> \(AM\) là đường phân giác của \(\widehat{A}.\)
b) Xét \(\Delta ABC\) có:
\(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại A.
Có \(AM\) là đường phân giác (cmt) đồng thời \(AM\) cũng là đường cao của \(\Delta ABC.\)
=> \(AM\) là đường cao của \(\Delta ABC.\)
c) Theo câu b) ta có \(\Delta ABC\) cân tại A.
Có \(AM\) là đường cao đồng thời \(AM\) cũng là đường trung trực của \(\Delta ABC.\)
=> \(AM\) là đường trung trực của \(BC.\)
Chúc bạn học tốt!

a)
Xét \(\Delta BHE\) và \(\Delta CHF\) có:
\(\widehat{B}=\widehat{C}\left(gt\right)\)
\(\widehat{E}=\widehat{F}=90^o\left(gt\right)\)
\(HB=HC\)( trong tam giác cân, đường cao cũng là đường trung tuyến)
\(\Rightarrow\Delta BHE=\Delta CHF\left(g.c.g\right)\)
\(\RightarrowĐpcm\)
a,C/m \(\Delta\) MNH la tam giác cân
Xét \(\Delta MNP\) :
MH là đường cao đồng thời là đường trung trực
=> \(\Delta MNP\) cân tại M
b, C/m MH là tia phân giác
\(\Delta MNP\) cân tại M => MH là đường trung trực đồng thơi là đường phân giác hay MH là tia phân giác của \(\widehat{NMP}\)