Tính gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai) :
a) \(16x^2-8x+1=0\)
b) \(6x^2-10x-1=0\)
c) \(5x^2+24x+9=0\)
d) \(16x^2-10+1=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
10 tháng 12 2019
5 x 2 +24x +9 =0
Ta có: ∆ ' = 12 2 -5.9 =144 - 45 =99 > 0
∆ ' = 99 = 3 11
Phương trình có 2 nghiệm phân biệt:
PT
1
CM
24 tháng 9 2017
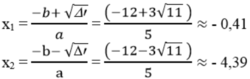
16 x 2 – 8x +1=0
Ta có: ∆ ' = - 4 2 – 16.1 = 16 -16 =0
Phương trình có nghiệm kép :
CM
3 tháng 6 2017
( 3 - x 5 )(2x 2 + 1) = 0 ⇔ 3 - x 5 = 0 hoặc 2x 2 + 1 = 0
3 - x 5 = 0 ⇔ x = 3 / 5 ≈ 0,775
2x 2 + 1 = 0 ⇔ x = - 1/2 2 ≈ - 0,354
Phương trình có nghiệm x = 0,775 hoặc x = - 0,354
CM
14 tháng 9 2019
a) x 2 = 2 = > x 1 = √ 2 v à x 2 = - √ 2
Dùng máy tính bỏ túi ta tính được:
√ 2 ≈ 1 , 414213562
Kết quả làm tròn đến chữ số thập phân thứ ba là:
x 1 = 1 , 414 ; x 2 = - 1 , 414 b ) x 2 = 3 = > x 1 = √ 3 v à x 2 = - √ 3
Dùng máy tính ta được:
√ 3 ≈ 1 , 732050907
Vậy x 1 = 1 , 732 ; x 2 = - 1 , 732
c) x 2 = 3 , 5 = > x 1 = √ 3 , 5 v à x 2 = - √ 3 , 5
Dùng máy tính ta được:
√ 3 , 5 ≈ 1 , 870828693
Vậy x 1 = 1 , 871 ; x 2 = - 1 , 871
d) x 2 = 4 , 12 = > x 1 = √ 4 , 12 v à x 2 = - √ 4 , 12
Dùng máy tính ta được:
√ 4 , 12 ≈ 2 , 029778313
Vậy x 1 = 2 , 030 ; x 2 = - 2 , 030
CM
15 tháng 5 2019
(2x - √2)2 – 1 = (x + 1)(x – 1);
⇔ 4x2 – 2.2x.√2 + 2 – 1 = x2 – 1
⇔ 4x2 – 2.2√2.x + 2 – 1 – x2 + 1 = 0
⇔ 3x2 – 2.2√2.x + 2 = 0
Có: a = 3; b’ = -2√2; c = 2; Δ’ = b’2 – ac = (-2√2)2 – 3.2 = 2 > 0
Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:
CM
28 tháng 2 2018
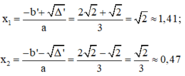
0,5x(x + 1) = (x – 1)2
⇔ 0,5x2 + 0,5x = x2 – 2x + 1
⇔ x2 – 2x + 1 – 0,5x2 – 0,5x = 0
⇔ 0,5x2 – 2,5x + 1 = 0
⇔ x2 – 5x + 2 = 0
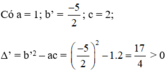
Phương trình có hai nghiệm phân biệt:
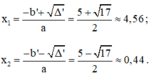
a: =>(4x-1)2=0
=>4x-1=0
hay x=1/4=0,25
b: \(6x^2-10x-1=0\)
\(\Delta=\left(-10\right)^2-4\cdot6\cdot\left(-1\right)=100+24=124>0\)
Do đó; Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{10-2\sqrt{31}}{12}\simeq-0,09\\x_2=\dfrac{10+2\sqrt{31}}{12}\simeq1,76\end{matrix}\right.\)
c: \(5x^2+24x+9=0\)
\(\Delta=24^2-4\cdot5\cdot9=396>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-24-2\sqrt{99}}{10}\simeq-4,39\\x_2=\dfrac{-24+2\sqrt{99}}{10}\simeq-0,41\end{matrix}\right.\)
d: \(16x^2-10x+1=0\)
\(\Delta=\left(-10\right)^2-4\cdot16\cdot1=100-64=36>0\)
Do đó: Phương trình có hai nghiệm phân biệt là
\(\left\{{}\begin{matrix}x_1=\dfrac{10-6}{64}=\dfrac{4}{64}=\dfrac{1}{16}\\x_2=\dfrac{10+6}{64}=\dfrac{1}{4}\end{matrix}\right.\)