xét xem các câu sau đây đúng hay sai
a, tam giác ABC có AB=BC thì góc C = góc A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TS
23 tháng 4 2023
Phát biểu a) là phát biểu sai. Vì một tam giác đều khi có ba cạnh bằng nhau không nhất thiết phải bằng 2cm, có thể bằng 3cm, 4cm, …
Phát biểu b) là đúng. Vì tam giác đều là tam giác có ba cạnh bằng nhau và ba góc bằng nhau.
Phát biểu c) là sai. Vì tam giác IKH chỉ có hai cạnh và hai góc bằng nhau nên chưa đủ điều kiện để tam giác IKH là tam giác đều.
help me
17 tháng 5 2022
a: \(\widehat{P}=180^0-80^0-60^0=40^0< \widehat{N}< \widehat{M}\)
nên MN<MP<NP
c: Đúng
d: Sai vì chỉ có tâm đường tròn ngoại tiếp cách đều 3 đỉnh thôi
CM
29 tháng 8 2019
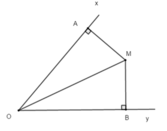
Gọi MA và MB theo thứ tự là khoảng cách từ M đến Ox và Oy
Xét hai tam giác vuông OMA và OMB có:
OM là cạnh chung
MA = MB (gt)
Do đó ΔOMA=ΔOMB (cạnh huyền – cạnh góc vuông)
Suy ra: M O A ^ = M O B ^ (hai góc tương ứng)
Vậy OM là tia phân giác của x O y ^
Vậy thứ tự sắp xếp phải là: b, c, a, d, e.
Chọn đáp án A
1 tháng 7 2015
Do tam giác ABC và A'B'C' có AB=A'B' ,AC=A'C'
Theo tính chất cạnh và góc đối diện,ta có:
Góc A >góc A' <=> BC>B'C' (đpcm)
b) tương tự như câu a ta có
BC>B'C' <=> Góc A >A'
22 tháng 6 2019
CM: Ta có: \(\widehat{BIM}+\widehat{MIN}+\widehat{NIC}=\widehat{BIC}\)
=> \(\widehat{BIC}=2.30^0+90^0=150^0\)
Ta lại có : \(\widehat{FIB}+\widehat{BIC}=180^0\) (kề bù)
=> \(\widehat{FIB}=180^0-\widehat{BIC}=180^0-150^0=30^0\)
=> \(\widehat{FIB}=\widehat{EIC}=30^0\) (đối đỉnh)
Xét t/giác FIB và t/giác MIB
có : \(\widehat{B_1}=\widehat{B_2}\) (gt)
BI : chung
\(\widehat{FIB}=\widehat{BIM}=30^0\)
=> t/giác FIB = t/giác MIB (g.c.g)
=> BF = BM (2 cạnh t/ứng)
Xét t/giác EIC và t/giác NIC
có : \(\widehat{C_1}=\widehat{C_2}\) (gt)
IC : chung
\(\widehat{EIC}=\widehat{NIC}=30^0\)
=> t/giác EIC = t/giác NIC (g.c.g)
=> EC = IN (2 cạnh t/ứng)
Ta có: BC = BM + MN + NC
hay BC = BF + MN + EC
=> CE + BF = BC - MN => CE + BF < BC (Đpcm)
tam giác ABC có AB = BC thì góc C = góc A là đúng ( quan hệ giữa góc và cạnh đối diện trong tam giác)
các pn ơi 1 tick cho mk nk!!!
câu trên đúng vì: AB = BC => t/g ABC cân tại B
=> góc C = góc A