Hình chóp lục giác đều S.ABCDEG có AB = 6cm, cạnh bên SA = 10cm. Vậy chiều cao hình chóp là :
(A) \(6cm\) (B) \(8cm\)
(C) \(\sqrt{91}cm\) (D) \(\sqrt{136}cm\)
Hãy chọn kết quả đúng ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi SO là đường cao của hình chóp
Khi đó △ AOB là tam giác đều cạnh
AB=6cm ⇒ OA=6cm
Trong tam giác vuông SOA áp dụng pi-ta-go ta tính được SO = 8cm
Vậy chọn đáp án B

a)
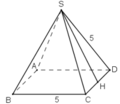
Ta có: các mặt bên của hình chóp đều là những tam giác đều cạnh 5cm. Đường cao của mỗi mặt bên:

b)
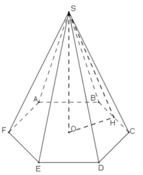
Mặt bên của hình chóp lục giác đều là tam giác cân có cạnh bên 10cm, cạnh đáy 6cm.

Diện tích toàn phần của hình chóp là:
Stp = Sxq + Sđ = 171,72 + 93,6 = 265,32(cm2)

Bài 7:
Chu vi đáy là: 6 x 3 = 18 cm
=> nửa chu vi đáy là: 18 : 2 = 9 cm
Diện tích xung quanh là: 9 x 10 = 90 cm vuông
Bài 8: Nửa chu vi là: 12 x 3 : 2 = 18 cm
Diện tích xung quanh là: 18 x 15 = 270 cm vuông
Diện tích đáy là: 12 x 12 : 2 = 72 cm vuông
Thể tích là: 1/3 x 72 x 12 = 288 cm khối
B