Hình 7
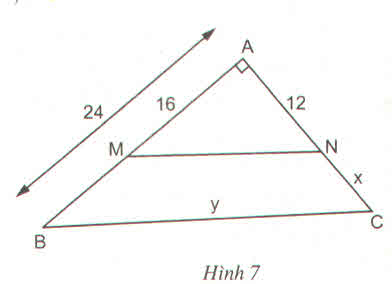
Cho biết tam giác ABC vuông tại A, MN // BC, AB = 24 cm, AM = 16 cm, AN = 12 cm. Tính độ dài x, y của các đoạn thẳng NC và BC ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Trong ΔABC, ta có: MN // BC (gt)
Suy ra: 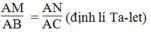
Suy ra: 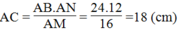
Vậy NC = AC – AN = 18 – 12 = 6(cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông AMN, ta có:
M N 2 = A M 2 + A N 2 = 16 2 + 12 2 = 400
MN = 20cm
Trong ΔABC, ta có: MN // BC (gt)
Suy ra:![]()
Vậy: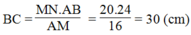

\(\Delta ABC\) có \(MN//BC\) áp dụng định lý Ta-lét ta có:
\(\frac{AM}{AB}=\frac{AN}{AC}\)
hay \(\frac{16}{24}=\frac{12}{AC}=\frac{MN}{BC}\)
\(\Rightarrow\)\(AC=\frac{24.12}{16}=18\) cm
Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=24^2+18^2=900\)
\(\Leftrightarrow\)\(BC=\sqrt{900}=30\)cm
Áp dụng định lí Ta-lét ta có:
\(\frac{MN}{BC}=\frac{AN}{AC}=\frac{AM}{AB}\Leftrightarrow\frac{MN}{BC}=\frac{12}{AC}=\frac{16}{24}=\frac{2}{3}\)
\(\Rightarrow\frac{12}{AC}=\frac{2}{3}\Leftrightarrow2AC=36\Leftrightarrow AC=18\left(cm\right)\)
\(AC=AN+NC\Leftrightarrow18=12+NC\Rightarrow NC=6\left(cm\right)\)
\(\text{ }\text{Áp dụng định lí Py-ta-go vào tam giác vuông ABC ta có:}\)
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow24^2+18^2=BC^2\)
\(\Leftrightarrow BC^2=900\Rightarrow BC=30\left(cm\right)\)
Vậy....