2√3 sin23x - cos6x = √3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.

\(\Leftrightarrow\sin^2x-\sin^22x+\sin^23x-\sin^24x=0\)
\(\Leftrightarrow\left(\sin x+\sin2x\right)\left(\sin2x-\sin x\right)+\left(\sin3x+\sin4x\right)\left(\sin4x-\sin3x\right)=0\)
\(\Leftrightarrow2\sin\dfrac{3}{2}x.\cos\dfrac{x}{2}.2\cos\dfrac{3}{2}x.\sin\dfrac{x}{2}+2\sin\dfrac{7}{2}x.\cos\dfrac{x}{2}.2\sin\dfrac{x}{2}\cos\dfrac{7}{2}x=0\)
\(\Leftrightarrow\sin3x.\sin x+\sin7x.\sin x=0\)
\(\Leftrightarrow\sin x\left(\sin3x+\sin7x\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sin x=0\\\sin3x=\sin\left(-7x\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\3x=-7x+k2\pi\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{k\pi}{5}\end{matrix}\right.\)

Chứng minh các biểu thức đã cho không phụ thuộc vào x.
f(x) = 1 ⇒ f′(x) = 0


\(A=3\left[\left(sin^2x+cos^2x\right)^2-2\cdot sin^2x\cdot cos^2x\right]-2\left[\left(sin^2x+cos^2x\right)^3-3\cdot sin^2x\cdot cos^2x\left(sin^2x+cos^2x\right)\right]\)
\(=3\left[1-2\cdot sin^2x\cdot cos^2x\right]-2\left[1-3\cdot sin^2x\cdot cos^2x\right]\)
\(=3-6\cdot sin^2x\cdot cos^2x-2+6\cdot sin^2x\cdot cos^2x\)
=1

A = cos 6 x + 3 sin 2 x . cos 2 x + 2 sin 4 α . cos 2 x + sin 4 α
= cos 6 x + 3.(1 - cos 2 x ) cos 4 x + 2 sin 4 α . cos 2 x + sin 4 α
= cos 6 x + 3 cos 4 x - 3 cos 6 x + 2. sin 4 α .(1 - sin 2 x ) + sin 4 α= cos 6 x + 3 cos 4 x - 3 cos 6 x + 2 sin 4 α - 2 sin 6 x + sin 4 α
= -2.( cos 6 x + sin 6 x ) + 3 cos 4 x + 3 sin 4 α
= -2.( cos 6 x + sin 6 x ) + 3.( cos 4 x + sin 4 α ) = 1
Vậy biểu thức A không phụ thuộc vào x.

\(pt\Leftrightarrow cos6x+3cos2x-4\left(2cos^2x-1\right)=0\)
\(\Leftrightarrow cos6x+3cos2x-4cos2x=0\)
\(\Leftrightarrow cos6x-cos2x=0\)
\(\Leftrightarrow-2sin4x.sin2x=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sin4x=0\\sin2x=0\end{matrix}\right.\)
\(\Leftrightarrow x=\dfrac{k\pi}{4}\)
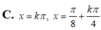
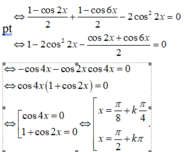
\(2\sqrt{3}\sin^23x-cos6x=\sqrt{3}\\ \Leftrightarrow2sin^23x\left(\sqrt{3}+1\right)=\sqrt{3}+1\\ \Leftrightarrow sin^23x=\dfrac{1}{2}\Leftrightarrow\dfrac{1-cos6x}{2}=\dfrac{1}{2}\Rightarrow cos6x=0\Leftrightarrow x=\pm\dfrac{\pi}{12}+k\dfrac{\pi}{6}\left(k\in Z\right)\)