Trong không gian tọa độ Oxyz, cho mp (P):2x-y+2z+9=0 và hai điểm A(3;-1;2), B(1;-5;0). Tìm tọa độ điểm M thuộc (P) sao cho \(\overrightarrow{MA}.\overrightarrow{MB}\) nhỏ nhất?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
29 tháng 12 2018
Chọn B.
Phương pháp : Số đo góc tạo bởi hai mặt phẳng hoặc bằng góc giữa hai véc tơ pháp tuyến hoặc bù với hai véc tơ pháp tuyến và góc giữa hai mặt phẳng là góc không tù.


CM
10 tháng 9 2019
Đáp án B
Ta có 2. 3-(-1)-2. 2-3=0 nên điểm Q(3; -1; 2) ∈ (P).
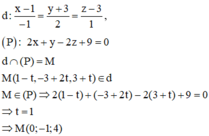
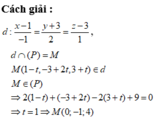

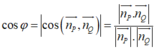
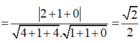

Lời giải:
Gọi \(I(a,b,c)\) là một điểm thỏa mãn \(\overrightarrow{IA}+\overrightarrow{IB}=0\)
\(\Rightarrow (3-a,-1-b,2-c)+(1-a,-5-b,-c)=0\Rightarrow I(2,-3,1)\)
Lại có:
\(P=\overrightarrow{MA}.\overrightarrow{MB}=(\overrightarrow{MI}+\overrightarrow{IA})(\overrightarrow{MI}+\overrightarrow{IB})=MI^2+\overrightarrow{IB}.\overrightarrow{IA}\)
\(\Leftrightarrow P=MI^2-6\)
Để \(P_{\min}\Leftrightarrow MI_{\min}\), điều đó đồng nghĩa với việc \(M\) là hình chiếu của $I$ lên mặt phẳng $(P)$
Gọi \(M(a,b,c)\Rightarrow \overrightarrow{IM}=(a-2,b+3,c-1)=k(2,-1,2)\)
\(\Rightarrow \frac{a-2}{2}=\frac{b+3}{-1}=\frac{c-1}{2}\)
Mặt khác, \(2a-b+2c+9=0\) nên \(a=-2,b=-1,c=-3\)
Vậy \(M(-2,-1,-3)\)