Chú ý nếu \(c>0\) thì \(\left(a+b\right)^2+c\) và \(\left(a-b\right)^2+c\) đều dương với mọi a, b
Áp dụng điều này chứng minh rằng :
a) Với mọi giá trị x khác \(\pm1\), biểu thức :
\(\dfrac{x+2}{x-1}.\left(\dfrac{x^3}{2x+2}+1\right)-\dfrac{8x+7}{2x^2-2}\) luôn có giá trị dương
b) Với mọi giá trị của x khác 0 và khác - 3, biểu thức :
\(\dfrac{1-x^2}{x}.\left(\dfrac{x^2}{x+3}-1\right)+\dfrac{3x^2-14x+3}{x^2+3x}\) luôn có giá trị âm


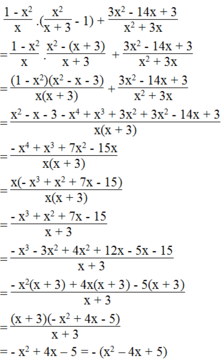
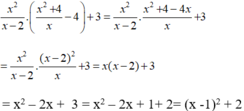
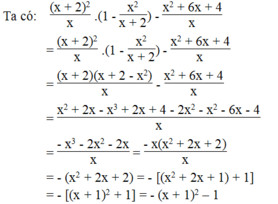

Vì \(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1\ge1>0\) với mọi giá trị của \(x\) nên giá trị của biểu thức luôn luôn âm với mọi giá trị khác 0 và khác -3 của \(x\)