Cho hai đa thức :
\(A=x^4-2x^3+x^2+13x-11\)
\(B=x^2-2x+3\)
Tìm thương A và dư R sao cho \(A=B.Q+R\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 4 2017
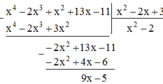
Thương Q = x 2 - 2
Dư R = 9x – 5
Ta thấy x 4 - 2 x 3 + x 2 + 13 x - 11 = ( x 2 - 2 x + 3 )( x 2 - 2 ) + (9x – 5)
Vậy A = B.Q + R
MP
1 tháng 9 2017
\(a.\frac{x^3-6x^2+12x-8+x^2-4x+4}{x-2}\)\(=\frac{\left(x-2\right)^3+\left(x-2\right)^2}{x-2}\)\(=2\left(x-2\right)^2\)
TH
0
CM
29 tháng 11 2019
a) A = ( x 2 – 6x)B.
b) A = (-x – 8)B + 2
c) A = (x + 3)B + 6.
8 tháng 11 2021
Bài 1:
\(=\dfrac{x^3-x^2+x+3}{x+1}\)
\(=\dfrac{x^3+x^2-2x^2-2x+3x+3}{x+1}\)
\(=x^2-2x+3\)
đây ạ