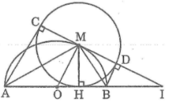
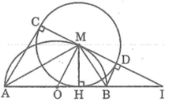
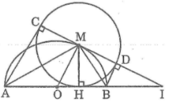
Cho nửa đường tròn O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đến AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M( C và D là các tiếp điểm khác H)
a) Chứng minh rằng ba điểm C, M, D thẳng hàng và CD là tiếp tuyến của đường tròn (O)
b) Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi
c) Giả sử CD và AB cắt nhau tại I. Chứng minh rằng tích OH.OI không đổi


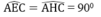
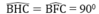
bạn ko chứng minh ABDC là hình thang ak?