S = 1+2+2^2+2^3+...+2^9; P = 5.2^8. So sánh S và P
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
1
NB
5
TL
2
N
24 tháng 3 2017
Ta có:\(S=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{9^2}\)
\(=\frac{1}{2.2}+\frac{1}{3.3}+\frac{1}{4.4}+...+\frac{1}{9.9}< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{8.9}\)
Mà \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{8.9}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{8}-\frac{1}{9}\)
\(=1-\frac{1}{9}\)
\(=\frac{8}{9}\)
Lại có \(S=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{9^2}\)
\(=\frac{1}{2.2}+\frac{1}{3.3}+\frac{1}{4.4}+...+\frac{1}{9.9}>\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}\)
Mà \(\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}\)
\(=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{9}-\frac{1}{10}\)
\(=\frac{1}{2}-\frac{1}{10}\)
\(=\frac{2}{5}\)
Vậy \(\frac{2}{5}< S< \frac{8}{9}\)
BT
24 tháng 3 2017
S< 1/1.2+1/2.3+1/3.4+...+1/8.9 = 1/1-1/2+1/2-1/3+1/3-1/4+...+1/8-1/9=1-1/9=8/9
=> S < 8/9
S> 1/2.3+1/3.4+1/4.5+...+1/9.10=1/2-1/3+1/3-1/4+1/4-1/5+...+1/9-1/10=1/2-1/10=4/10=2/5
=> S > 2/5
Đs: 2/5 < S < 8/9
TH
1
15 tháng 8 2018
\(\frac{1}{2\cdot2}< \frac{1}{1\cdot2};...;\frac{1}{9\cdot9}< \frac{1}{8\cdot9}\)
\(\Rightarrow S=\frac{1}{2^2}+...+\frac{1}{9^2}< \frac{1}{1\cdot2}+...+\frac{1}{8\cdot9}=1-\frac{1}{2}+...+\frac{1}{8}-\frac{1}{9}=1-\frac{1}{9}=\frac{8}{9}\left(1\right)\)
\(\frac{1}{2\cdot2}>\frac{1}{2\cdot3};...;\frac{1}{9\cdot9}>\frac{1}{9\cdot10}\)
\(\Rightarrow S=\frac{1}{2^2}+...+\frac{1}{9^2}>\frac{1}{2\cdot3}+...+\frac{1}{9\cdot10}=\frac{1}{2}-\frac{1}{3}+...+\frac{1}{9}-\frac{1}{10}=\frac{1}{2}-\frac{1}{10}=\frac{2}{5}\left(2\right)\)
Từ (1)(2) => đpcm
TH
1
AH
Akai Haruma
Giáo viên
26 tháng 10
Lời giải:
$S=\frac{1}{2^2}+\frac{3^2}+\frac{1}{4^2}+...+\frac{1}{9^2}$
$> \frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+....+\frac{1}{9.10}$
$=\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{9}-\frac{1}{10}$
$=\frac{1}{2}-\frac{1}{10}=\frac{2}{5}(*)$
Lại có:
$S=\frac{1}{2^2}+\frac{3^2}+\frac{1}{4^2}+...+\frac{1}{9^2}$
$< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+....+\frac{1}{8.9}$
$=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{8}-\frac{1}{9}=1-\frac{1}{9}=\frac{8}{9}(**)$
Từ $(*); (**)$ ta có đpcm.
NL
0
HT
1
14 tháng 4 2019
S<1/2^2 + 1/2.3 + 1/3.4 +...+ 1/8.9
S<1/4 + 1/2 - 1/3 + 1/3 - 1/4+...+1/8 - 1/9
S<1/4 + 1/2 - 1/9
S<23/36<8/9 (1)
Mặt khác: S>1/2^2 + 1/3.4 + ...+ 1/9*10
S>1/4 + 1/3 - 1/4 + ... + 1/9 - 1/10
S>1/4 + 1/3 - 1/10
S>29/60>2/5 (2)
Từ (1),(2)
=> 2/5<S<8/9
15 tháng 1 2023
Tính các tổng sau:
1, S=1-2+3_4+..+25-26
S =-1+3-5+7-...-53+55 ( có 28 số hạng )
= (-1+3)+(-5+7)+...+(-53+55) ( có 28:2=14 nhóm )
= 2+2+...+2
= 2 . 14
= 28
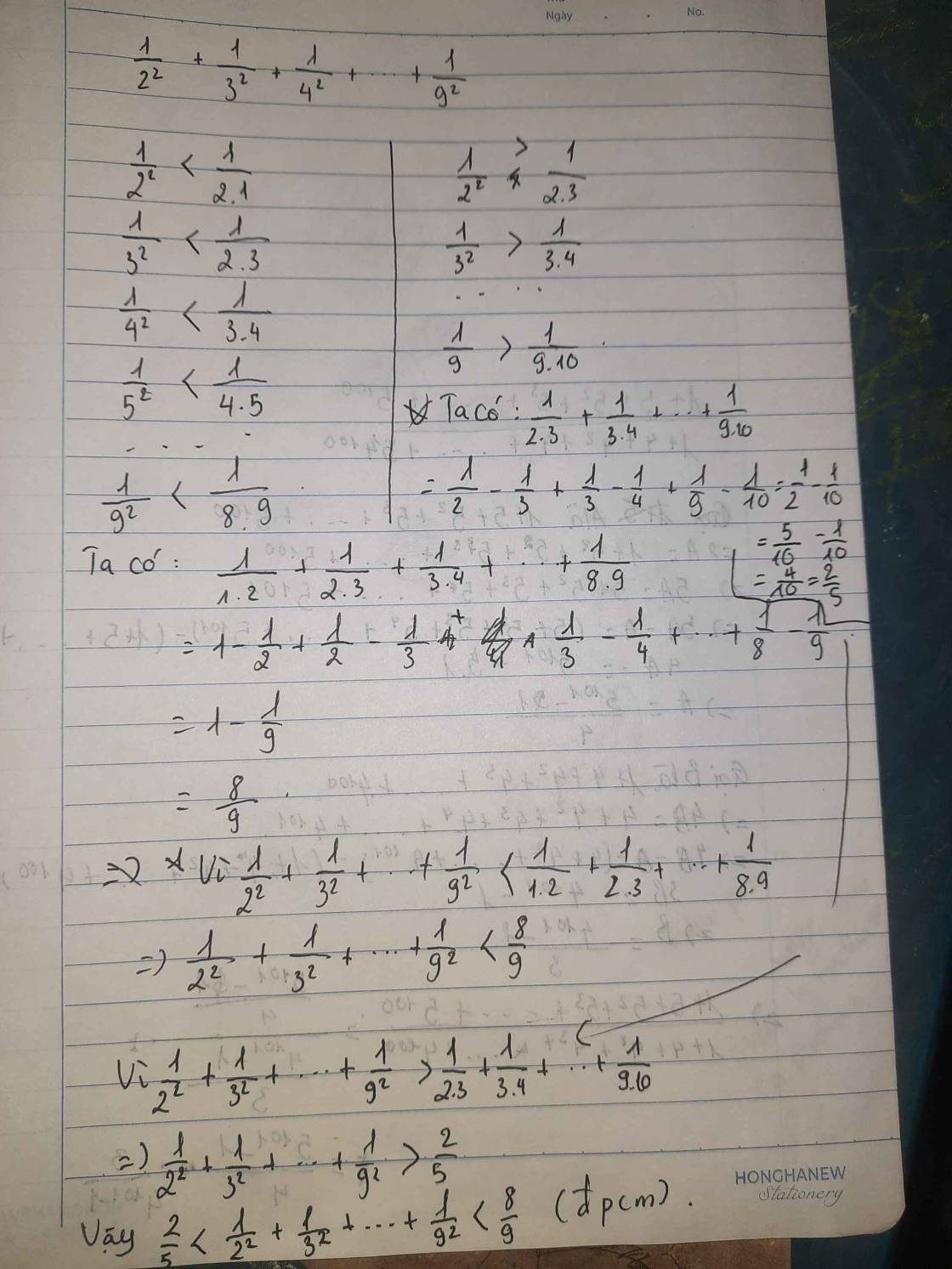
2S = 2+22+23+24+...+210
2S - S = S = 210-1
S = 28.22-1
S = 28.4 - 1
Ta có:
5.28 > 28.4 > 28.4 - 1
=> 5.28 > 28.4-1
=> P > S
=> S < P
S= \(2^{10}-1\)
\(P=\left(2^2+1\right)2^8=2^{10}+2^8\)
S < P