Hãy tìm \(\sin\alpha,\cos\alpha\) (làm tròn đến chữ số thập phân thứ tư) nếu biết :
a) \(tg\alpha=\dfrac{1}{3}\)
b) \(cotg\alpha=\dfrac{3}{4}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: sin2α + cos2α = 1
Suy ra: sin2α = 1 – cos2α = 1 – (0,8)2 = 1 – 0,64 = 0,36
Vì sin α > 0 nên sin α = √0,36 = 0,6
Suy ra: tg α = sinα/cosα = 0,6/0,8 = 3/4 = 0,75
cotg α = 1/tgα = 1/0,75 = 1,3333

Bài 2:
\(\cos a=\sqrt{1-\left(\dfrac{7}{25}\right)^2}=\dfrac{24}{25}\)
\(\tan a=\dfrac{7}{25}:\dfrac{24}{25}=\dfrac{7}{24}\)
\(\cot a=\dfrac{24}{7}\)

a, Ta có tổng các góc bằng 180o
=> \(\widehat{P}=55^o\)
- Áp dụng tỉ số lượng giác :
\(\cos35=\dfrac{MN}{4}\)
\(\Rightarrow MN\approx3,277cm\)
\(\sin35=\dfrac{MP}{4}\)
\(\Rightarrow MP\approx2,294cm\)
b, Ta có : \(A=\dfrac{2\cos^2a-\cos^2a-\sin^2a}{\sin a+\cos a}=\dfrac{\left(\sin a+\cos a\right)\left(\cos a-\sin a\right)}{\sin a+\cos a}\)
\(=\cos a-\sin a\)
c, \(sin30< sin35< cos40< sin60< cos25\)

a) Cần chứng minh \(\dfrac{1-cos\alpha}{sin\alpha}=\dfrac{sin\alpha}{1+cos\alpha}\)
\(\Rightarrow sin^2\alpha=\left(1-cos\alpha\right)\left(1+cos\alpha\right)\Rightarrow sin^2\alpha=1-cos^2\alpha\)
\(\Rightarrow sin^2\alpha+cos^2\alpha=1\)
Giả sử tam giác ABC vuông tại A
Ta có: \(\left\{{}\begin{matrix}sin^2B=\dfrac{AC^2}{BC^2}\\cos^2B=\dfrac{AB^2}{BC^2}\end{matrix}\right.\Rightarrow sin^2B+cos^2B=\dfrac{AC^2+AB^2}{BC^2}=\dfrac{BC^2}{BC^2}=1\)
a)\(\dfrac{1-cosa}{sina}=\dfrac{sina}{1+cosa}\)
<=>\(\left(1-cosa\right)\left(1+cosa\right)=sin^2a\)
<=>\(1-cos^2a=sin^2a\) (lđ)
b)Ta có VT=\(\dfrac{cosa}{1+sina}+tga=\dfrac{cosa}{1+sina}+\dfrac{sina}{cosa}=\dfrac{cos^2a+sin^2a+sina}{\left(1+sina\right)cosa}=\dfrac{1+sina}{\left(1+sina\right)cosa}=\dfrac{1}{cosa}=vp\left(dpcm\right)\)

Vì tg α = 1/3 nên α là góc nhọn của một tam giác vuông có các cạnh góc vuông là 1 và 3.
Suy ra cạnh huyền của tam giác vuông là: ![]() = 3,1623
= 3,1623
Vậy: sin α = 3/5 ≈ 0,6 cos α = 4/5 ≈ 0,8

Hướng dẫn giải:
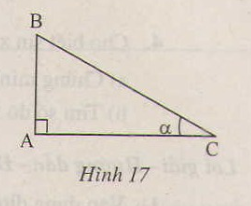
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.
Đặt \(x=\alpha\)
a: \(\dfrac{1}{\cos^2x}=1+\tan^2x=1+\dfrac{1}{9}=\dfrac{10}{9}\)
nên \(\cos x=\dfrac{3\sqrt{10}}{10}\)
=>\(\sin x=\dfrac{\sqrt{10}}{10}\)
b: \(\dfrac{1}{\sin^2x}=1+\cot^2x=1+\dfrac{9}{16}=\dfrac{25}{16}\)
\(\Leftrightarrow\sin x=\dfrac{4}{5}\)
hay \(\cos x=\dfrac{3}{5}\)