Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
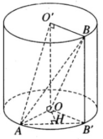
Ta có ( α ) là (ABB’). Vì OO’ // ( α ) nên khoảng cách giữa OO’ và ( α ) bằng khoảng cách từ O đến ( α ). Dựng OH ⊥ AB′ ta có OH ⊥ ( α ).
Vậy khoảng cách cần tìm là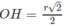 
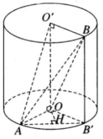
Đường tròn tâm O có bán kính bằng r 2 2 tiếp xúc với AB’ tại H là trung điểm của AB’. Do đó mặt phẳng ( α ) song song với trục OO’ chứa tiếp tuyến của đường tròn đáy, nên ( α ) tiếp xúc với mặt trụ dọc theo một đường sinh, với mặt trụ có trục OO’ và có bán kính đáy bằng r 2 2
a:
I nằm giữa O và A
=>OI+IA=OA
=>OI=OA-AI
=R-R'
=>(O) với (I) tiếp xúc nhau tại A
b: ΔIAD cân tại I
=>góc IAD=góc IDA
=>góc IDA=góc OAC
ΔOAC cân tại O
=>góc OAC=góc OCA
=>góc IDA=góc OCA
mà hai góc này đồng vị
nên ID//OC
c: Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó; ΔACB vuông tại C
Xét ΔACB vuông tại C có cos CAB=AC/AB=1/2*căn 3
=>góc CAB=30 độ
CB=căn AB^2-AC^2=R/2
\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{R\sqrt{3}}{2}\cdot\dfrac{1}{2}R=\dfrac{R^2\sqrt{3}}{8}\)
Xét ΔADO vuông tại D và ΔACB vuông tại C có
góc DAO chung
Do đó: ΔADO đồng dạng với ΔACB
=>\(\dfrac{S_{ADO}}{S_{ACB}}=\left(\dfrac{AO}{AB}\right)^2=\left(\dfrac{1}{4}\right)\)
=>\(S_{ODCB}=\dfrac{3}{4}\cdot S_{ACB}=\dfrac{3}{4}\cdot\dfrac{R^2\sqrt{3}}{8}=\dfrac{3\cdot\sqrt{3}\cdot R^2}{32}\)
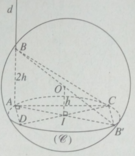
Ta có AH ⊥ DC. Do đó khi CD di động, điểm H luôn luôn nhìn đọan thẳng AI dưới một góc vuông. Vậy tập hợp các điểm H là đường tròn đường kính AI nằm trong mặt phẳng ( α ).
Chọn A
Tìm tâm I và bán kính R của mặt cầu. Tâm J của đường tròn là hình chiếu vuông góc của I trên mặt phẳng α . Bán kính của đường tròn r = R 2 - d 2 với d là khoảng cách từ I đến .
Giả sử vẽ được như hình bs.18
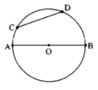
Dùng compa so sánh được CD < AB.
và mặt phẳng
(
α
)
:
2
x
-
2
y
-
z
+
9
=
0
.Mặt phẳng
(
α
)
cắt mặt cầu (S) theo một đường tròn (C). Tìm tọa độ tâm J và bán kính r của đường tròn (C).
Bài làm đúng phong cách trắc nghiệm
A) loại
B) xét (lọai kiểu gì phải có góc \(\left(\pi-\alpha\right)\)
C) loại kiểu gì phải có yếu tố d+d=2d
D) xét có đủ yếu tố => duy nhất có thể nếu không đúng => đề sai
Chọn (D)
Lời giải
kéo dài OO' cắt vòng tròn bên Phải tại D cắt vòng tron bên trái tai C
Góc BOC =pi-anpha
góc AOD =alpha
\(L=2\left(L_1+L_2+L_3\right)\)
\(\left\{{}\begin{matrix}L_1=d\\L_2=AO.\alpha=\alpha r\\L_3=BO'.\left(\pi-\alpha\right)=\left(\pi-\alpha\right)R\end{matrix}\right.\)