Phát biểu các tính chất của hình thang ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 5 2017
Tính chất:
- Định lí 1: Trong hình thang cân, hai cạnh bên bằng nhau.
- Định lí 2: Trong hình thang cân, hai đường chéo bằng nhau.
CM
15 tháng 10 2017
- Đường trung bình của tam giác:
+ Định lí 1: Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.
+ Định lí 2: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
- Đường trung bình của hình thang:
+ Định lí 3: Đường thẳng đi qua trung điểm của một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.
+ Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.
HY
21 tháng 4 2017
• Đường trung bình của tam giác song song với cạnh thứ 3 và bằng nửa cạnh ấy.
• Đường trung bình của hình thang song song với 2 đáy và bằng nửa tổng 2 đáy.
PT
1
CM
7 tháng 1 2018
Tính chất:
- Hình bình hành:
Trong hình bình hành:
a) Các cạnh đối bằng nhau.
b) Các góc đối bằng nhau.
c) Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
- Hình chữ nhật:
Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.
- Hình thoi:
Trong hình thoi:
a) Hai đường chéo vuông góc với nhau.
b) Hai đường chéo là các đường phân giác của các góc của hình thoi.
- Hình vuông:
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
SG
3
21 tháng 4 2017
- Hình chữ nhật có tính chất :
+ Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường + Tất cả các tính chất của hình thang cân và hình thoi. - Hình thoi có tính chất : + Hai đường chéo vuông góc với nhau + Hai đường chéo là các đường phân giác của các góc của hình thoi và cắt nhau tại trung điểm của mỗi đường + Tất cả các tính chất của hình bình hành- Hình bình hành có tính chất:
+ Các cạnh đối bằng nhau + Các góc đối bằng nhau + Hai đường chéo cắt nhau tại trung điểm của mỗi đường Hình vuông có tính chất : - Hình vuông có các tính chất của hình chữ nhật và hình thoi.
20 tháng 7 2021
Tham khảo:
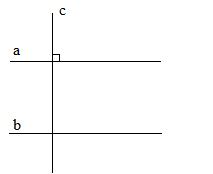
Hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song với nhau (hình a)
a⊥c;b⊥c⇒a//ba⊥c;b⊥c⇒a//b
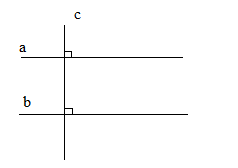
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia (hình b)
a//b;c⊥a⇒c⊥ba//b;c⊥a⇒c⊥b
Hai đường thẳng phân biệt cùng song song với một đường thnửg thứ ba thì chúng song song với nhau (hình c)
a // c; b // c ⇒⇒ a // b
CM
11 tháng 2 2017
Hai đường thẳng phân biệt vuông góc với đường thẳng thứ ba thì chúng song song với nhau (hình a)
a⊥ c;b⊥c⇒ a//b
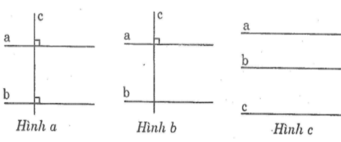
Một đường thẳng vuông góc với một trong hai đường thẳng song song thì nó cũng vuông góc với đường thẳng kia (hình b)
a//b; c⊥ a⇒ c ⊥ b
Hai đường thẳng phân biệt cùng song song với một đường thẳng thứ ba thì chúng song song với nhau (hình c)
a//c; b//c ⇒ a//b
Tính chất: Trong hình thang hai cạnh đáy song song với nhau.
Hình thang có 2 cạnh đáy song song với nhau