Question

[Sách Giáo Khoa]

Đố :

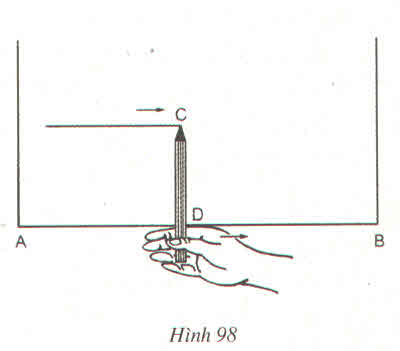
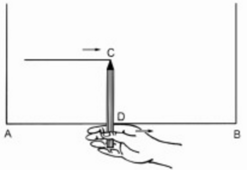
Để vạch một đường thẳng song song với mép gỗ AB và cách mép gỗ 10 cm, bác thợ mộc đặt đoạn bút chì CD dài 10 cm vuông góc với ngón tay trỏ lấy làm cữ (h.98), rồi đưa ngón trỏ chạy dọc theo mép gỗ AB. Căn cứ vào kiến thức nào mà ta kết luận được rằng đầu chì C vạch nên đường thẳng song song với AB và cách AB là 10 cm ?

Answer 1

[Thien Tu Borum]

Bài giải:

Căn cứ vào tính chất đưởng thẳng song song với một đường thẳng cho trước ta kết luận là vì điểm C cách mép gỗ AB một khoảng bằng 10cm nên đầu chì C vạch nên đường thằng song song với AB và cách AB một khoảng 10cm.

Answer 2

[Nguyễn Đinh Huyền Mai]

Căn cứ vào tính chất đưởng thẳng song song với một đường thẳng cho trước ta kết luận là vì điểm C cách mép gỗ AB một khoảng bằng 10cm nên đầu chì C vạch nên đường thằng song song với AB và cách AB một khoảng 10cm.