cho hàm số y=2x-4 có đồ thị là (d)
a)vẽ đồ thị (d) của hàm số
b)tìm toạ độ giao điểm m của (d) và đường thẳng y=8-x bằng phép tính
c)tính góc tạo bởi đường thẳng y=2x-4 với trục Ox
mấy bạn làm giúp ạ, mình đang cần gấp:(
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 9 2023
a) \(\left\{{}\begin{matrix}\left(d\right):y=-2x-5\\\left(d'\right):y=-x\end{matrix}\right.\)
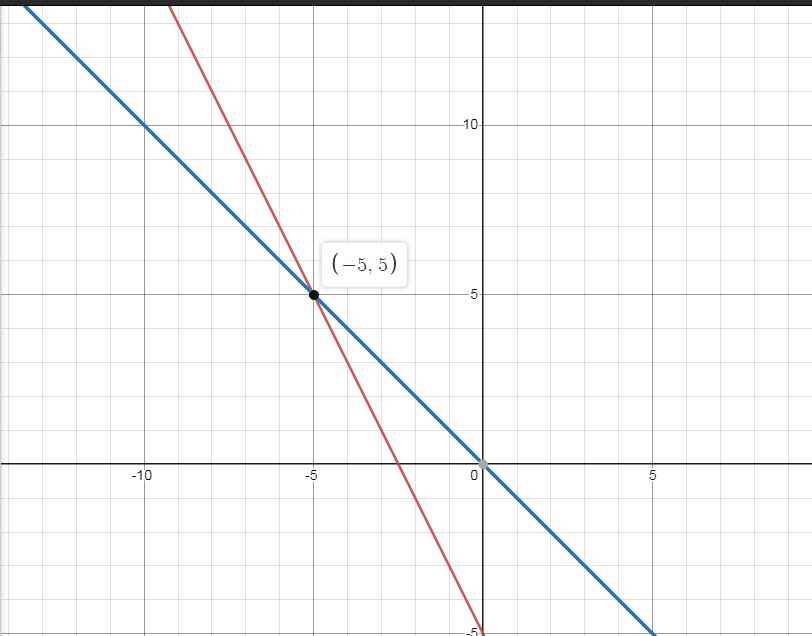
b) \(\left(d\right)\cap\left(d'\right)=M\left(x;y\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
\(\Rightarrow M\left(-5;5\right)\)
c) Gọi \(\widehat{M}=sđ\left(d;d'\right)\)
\(\left(d\right):y=-2x-5\Rightarrow k_1-2\)
\(\left(d'\right):y=-x\Rightarrow k_1-1\)
\(tan\widehat{M}=\left|\dfrac{k_1-k_2}{1+k_1.k_2}\right|=\left|\dfrac{-2+1}{1+\left(-2\right).\left(-1\right)}\right|=\dfrac{1}{3}\)
\(\Rightarrow\widehat{M}\sim18^o\)
19 tháng 9 2023
d) \(\left(d\right)\cap Oy=A\left(0;y\right)\)
\(\Leftrightarrow y=-2.0-5=-5\)
\(\Rightarrow A\left(0;-5\right)\)
\(OA=\sqrt[]{0^2+\left(-5\right)^2}=5\left(cm\right)\)
\(OM=\sqrt[]{5^2+5^2}=5\sqrt[]{2}\left(cm\right)\)
\(MA=\sqrt[]{5^2+10^2}=5\sqrt[]{5}\left(cm\right)\)
Chu vi \(\Delta MOA:\)
\(C=OA+OB+MA=5+5\sqrt[]{2}+5\sqrt[]{5}=5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)\left(cm\right)\)
\(\Rightarrow p=\dfrac{C}{2}=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}p-OA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5=\dfrac{5\left(\sqrt[]{2}+\sqrt[]{5}-1\right)}{2}\\p-OB=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{2}=\dfrac{5\left(-\sqrt[]{2}+\sqrt[]{5}+1\right)}{2}\\p-MA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{5}=\dfrac{5\left(\sqrt[]{2}-\sqrt[]{5}+1\right)}{2}\end{matrix}\right.\)
\(p\left(p-MA\right)=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}.\dfrac{5\left(1+\sqrt[]{2}-\sqrt[]{5}\right)}{2}\)
\(\Leftrightarrow p\left(p-MA\right)=\dfrac{25\left[\left(1+\sqrt[]{2}\right)^2-5\right]}{4}=\dfrac{25.2\left(\sqrt[]{2}-1\right)}{4}=\dfrac{25\left(\sqrt[]{2}-1\right)}{2}\)
\(\left(p-OA\right)\left(p-OB\right)=\dfrac{25\left[5-\left(\sqrt[]{2}-1\right)^2\right]}{4}\)
\(\Leftrightarrow\left(p-OA\right)\left(p-OB\right)=\dfrac{25.2\left(\sqrt[]{2}+1\right)}{4}=\dfrac{25\left(\sqrt[]{2}+1\right)}{4}\)
Diện tích \(\Delta MOA:\)
\(S=\sqrt[]{p\left(p-OA\right)\left(p-OB\right)\left(p-MA\right)}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25\left(\sqrt[]{2}-1\right)}{2}.\dfrac{25\left(\sqrt[]{2}+1\right)}{2}}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25^2}{2^2}}=\dfrac{25}{2}=12,5\left(cm^2\right)\)
10 tháng 5 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x^2-2x-1=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-3x+x-1=0\\y=3x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(3x+1\right)=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;3\right);\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\right\}\)
KT
6 tháng 1 2019
Bài 1:
Đặt: (d): y = (m+5)x + 2m - 10
Để y là hàm số bậc nhất thì: m + 5 # 0 <=> m # -5
Để y là hàm số đồng biến thì: m + 5 > 0 <=> m > -5
(d) đi qua A(2,3) nên ta có:
3 = (m+5).2 + 2m - 10
<=> 2m + 10 + 2m - 10 = 3
<=> 4m = 3
<=> m = 3/4
KT
6 tháng 1 2019
(d) cắt trục tung tại điểm có tung độ bằng 9 nên ta có:
9 = (m+5).0 + 2m - 10
<=> 2m - 10 = 9
<=> 2m = 19
<=> m = 19/2
(d) đi qua điểm 10 trên trục hoành nên ta có:
0 = (m+5).10 + 2m - 10
<=> 10m + 50 + 2m - 10 = 0
<=> 12m = -40
<=> m = -10/3
(d) // y = 2x - 1 nên ta có:
\(\hept{\begin{cases}m+5=2\\2m-10\ne-1\end{cases}}\) <=> \(\hept{\begin{cases}m=-3\\m\ne\frac{9}{2}\end{cases}}\) <=> \(m=-3\)
13 tháng 2 2022
a: Vì (d)//y=2x+3 nên a=2
Vậy: y=2x+b
Thay x=1 và y=-2 vào (d), ta được:
b+2=-2
hay b=-4
Vậy: (d): y=2x-4
c: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-4x+3=2x-4\\y=2x-4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{6}\\y=-\dfrac{5}{3}\end{matrix}\right.\)
d: Vì hai đường song song nên 2m-3=2
=>2m=5
hay m=5/2
SG
30 tháng 4 2023
a, (d) cắt trục hoành tại A(xA;0) và trục tung B(0;xB)
Vì A thuộc (d) nên \(0=-2x_A+4\Leftrightarrow x_A=2 \Rightarrow A(2;0)\)
Vì B thuộc (d) nên \(y_B=-2.0+4=4\Rightarrow B(0;4)\)
Vậy A(2;0) và B(0;4) là hai điểm cần tìm.
b, Gọi C(xc;yc) là điểm có hoành độ bằng tung độ
⇒ xc = yc = a. Vì C thuộc (d) nên \(a=-2a+4\Leftrightarrow a=\dfrac{4}{3}\)
⇒ \(C(\dfrac{4}{3};\dfrac{4}{3})\) là điểm cần tìm.
xem trc câu a,c để mk làm đề nha