1.
a) Vẽ vào vở ΔABC, biết AB = 2,5 cm ; AC = 3,5 cm ; BC = 7 cm .
b) Vẽ vào vở ΔEFG , có EF = FG = GE = 3 cm . Sau đó đo ba góc của tam giác EFG rồi cho biết số đo của mỗi góc .
c) Sắp xếp lại trình tự các bước chứng minh bài toán sau
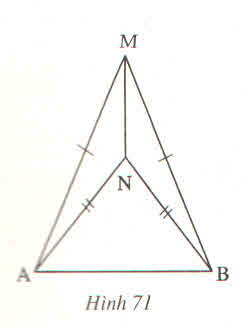
Bài toán : " ΔAMB và ΔANB có MA = MB , NA = NB ( h.69 ) . Chứng minh rằng ∠AMN = ∠ BMN " .
Các bước chứng minh :
i) Do đó ΔAMN = ΔBMN ( c.c.c )
ii) MN : cạnh chung ;
MA = MB ( giả thiết )
NA = NB...
Đọc tiếp
1.
a) Vẽ vào vở ΔABC, biết AB = 2,5 cm ; AC = 3,5 cm ; BC = 7 cm .
b) Vẽ vào vở ΔEFG , có EF = FG = GE = 3 cm . Sau đó đo ba góc của tam giác EFG rồi cho biết số đo của mỗi góc .
c) Sắp xếp lại trình tự các bước chứng minh bài toán sau
Bài toán : " ΔAMB và ΔANB có MA = MB , NA = NB ( h.69 ) . Chứng minh rằng ∠AMN = ∠ BMN " .
Các bước chứng minh :
i) Do đó ΔAMN = ΔBMN ( c.c.c )
ii) MN : cạnh chung ;
MA = MB ( giả thiết )
NA = NB ( giả thiết )
iii) Suy ra ∠AMN = ∠BMN (hai góc tương ứng )
iv) ΔAMN và ΔBMN có :
2 . a) Ví dụ
Cho hình 70 , chứng minh DE là tia phân giác của ∠ADB .
Xét ΔADE và ΔBDE , từ hình vẽ ta có :
AD = BD ; AE = BE ; DE là cạnh chung.
Do đó ΔADE = ΔBDE ( c.c.c ) , suy ra ∠ADE = ∠BDE ( hai góc tương ứng ) .
b) Em hãy giải bài toán sau và viết vào vở như ví dụ trên .
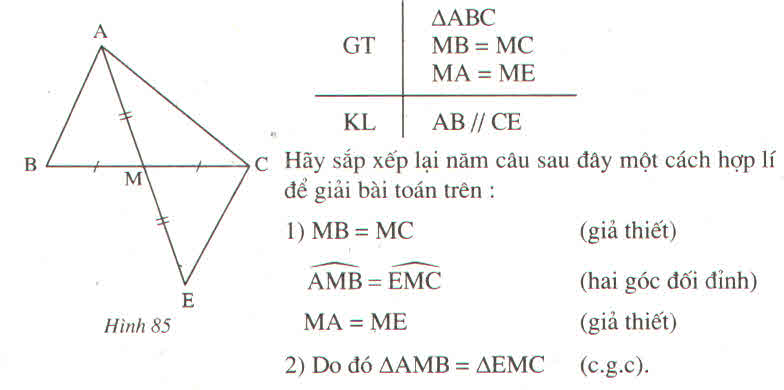
Bài toán : Cho đoạn thẳng AB = 5 cm . Vẽ đường tròn tâm A bán kính 3 cm và đường tròn tâm B bán kính 4,5 cm , chúng cắt nhau ở C và D . Chứng minh rằng AB là tia phân giác của góc CAD .

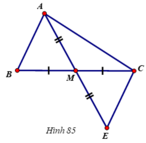
 5) Tam giác AMB và tam giác EMC có
5) Tam giác AMB và tam giác EMC có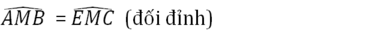



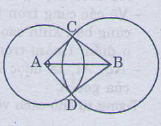


Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg