Cho các đa thức :
\(P\left(x\right)=x^5-2x^4+x^2-x+1\)
\(Q\left(x\right)=6-2x+3x^3+x^4-3x^5\)
Tính \(P\left(x\right)-Q\left(x\right)\) và \(Q\left(x\right)-P\left(x\right)\) ?
Có nhận xét gì về các hệ số của hai đa thức tìm được ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

P (x) = x5 + 2x4 + x2 - x +1
Q (x) = 6 - 2x + 3x3 + x4 - 3x5
P (x) - Q (x) = (x5 + 2x4 + x2 - x +1) - ( 6 - 2x + 3x3 + x4 - 3x5)
= x5 + 2x4 + x2 - x +1 - 6 + 2x - 3x3 - x4 + 3x5
= ( x5 + 3x5 ) + ( 2x4 - x4 ) - 3x3 + x2 + ( -x + 2x ) +( 1 - 6 )
= 4x5 + x4 - 3x3 + x2 + x - 5
Q (x) - P (x) = ( 6 - 2x + 3x3 + x4 - 3x5 ) - (x5 + 2x4 + x2 - x +1)
= 6 - 2x + 3x3 + x4 - 3x5 - x5 - 2x4 - x2 + x -1
= - ( 3x5 + x5 ) + ( x4 - 2x4 ) + 3x3 - x2 - ( 2x - x ) + ( 6 - 1)
= - 4x5 - x4 + 3x3 - x2 - x + 5
* Nhận xét: Hệ số của hai đa thức P (x) và Q(x) đối nhau.

a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
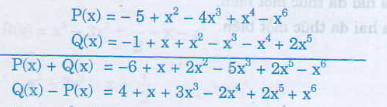 .
.
a) Sắp xếp các hạng tử của mỗi đa thức theo lũy thừa tăng của biến.
Thu gọn: P(x) = 3x2 - 5 + x4 - 3x3 - x6 - 2x2 - x3
= x2 - 5 + x4 - 4x3 - x6
Sắp xếp: P(x) = -5 + x2 - 4x3 + x4 - x6
Thu gọn: Q(x) = x3 + 2x5 - x4 + x2 - 2x3 + x - 1= -x3 +2x5 - x4 + x2 + x - 1
Sắp xếp: Q(x) = -1 + x + x2 - x3 - x4 + 2x5
b) Ta có:
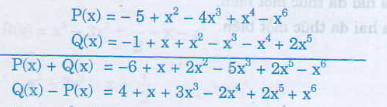

\(f\left(x\right)+h\left(x\right)-g\left(x\right)\)
\(=\left(5x^4+3x^2+x-1\right)+\left(-x^4+3x^3-2x^2-x+2\right)\)
\(-\left(2x^4-x^3+x^2+2x+1\right)\)
\(=\left(5x^4-x^4-2x^4\right)+\left(3x^3+x^3\right)+\left(3x^2-2x^2-x^2\right)\)
\(+\left(x-x-2x\right)+\left(-1+2-1\right)\)
\(=2x^4+4x^3-2x\)

\(3x^4-4x^3+2x\left(x^3-2x^2+7x\right)\)
\(=3x^4-4x^3+2x^4-4x^3+14x^2\)
\(=5x^4-8x^3+14x^2\)
3x4 - 4x3 + 2x(x3 - 2x2 + 7x )
= 3x4 - 4x3 + 2x4 _ 4x3 + 14x2
= 5x4 - 8x3 + 14x2

1,
a,\(2x\left(3x^2-5x+3\right)\)
\(=6x^3-10x^2+6x\)
b,\(-2x\left(x^2+5x-3\right)\)
\(=-2x^3-10x^2+6x\)
c,\(-\dfrac{1}{2}x\left(2x^3-4x+3\right)\)
\(=-x^4+2x^2-\dfrac{3}{2}x\)
Bài 2:
a) \(\left(2x-1\right)\left(x^2-5-4\right)\)
\(=\left(2x-1\right)\left(x^2-9\right)\)
\(=2x^3-18x-x^2+9\)
b) \(-\left(5x-4\right)\left(2x+3\right)\)
\(=-\left(10x^2+15x-8x-12\right)\)
\(=-10x^2-7x+12\)
c) \(\left(2x-y\right)\left(4x^2-2xy+y^2\right)\)
\(=8x^3-y^3\)

Lời giải:
a)
\(x(2x+1)-x^2(x+3)+x^3-x+3=2x^2+x-x^3-2x^2+x^3-x+3\)
\(=3\) không phụ thuộc vào biến (đpcm)
b)
\(4(x-6)-x^2(2+3x)+x(5x-4)+3x^2(x-1)\)
\(=4x-24-2x^2-3x^3+5x^2-4x+3x^3-3x^2\)
\(=(4x-4x)-24+(-2x^2+5x^2-3x^2)+(-3x^3+3x^3)\)
\(=-24\) không phụ thuộc vào biến.
c)
\((x^2+2x+3)(3x^2-2x+1)-3x^2(x^2+2)-4x(x^2-1)\)
\(=(3x^4-2x^3+x^2+6x^3-4x^2+2x+9x^2-6x+3)-(3x^4+6x^2)-(4x^3-4x)\)
\(=(3x^4-3x^4)+(-2x^3+6x^3-4x^3)+(x^2-4x^2+9x^2-6x^2)+(2x-6x+4x)+3\)
\(=3\) không phụ thuộc vào biến (đpcm)
Nhận xét: Các hệ số tương ứng của hai đa thức tìm được đối nhau.