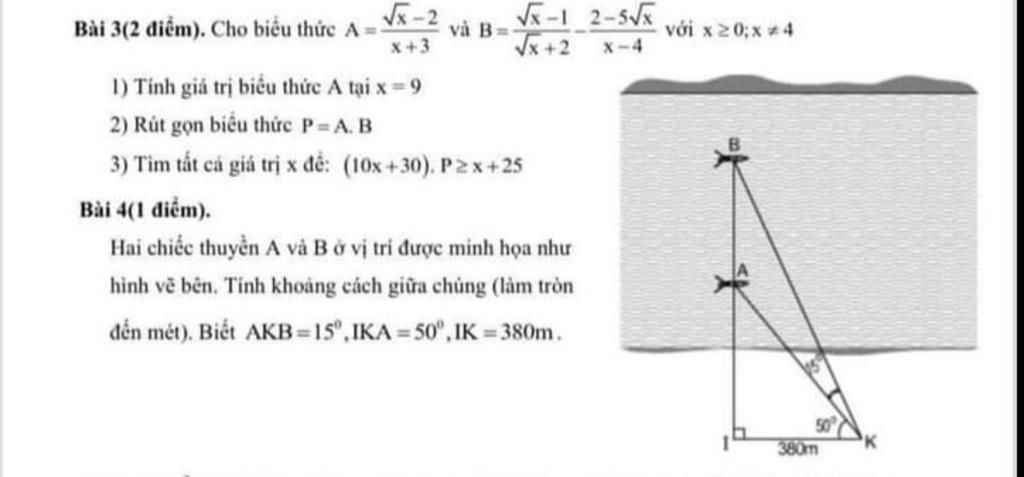
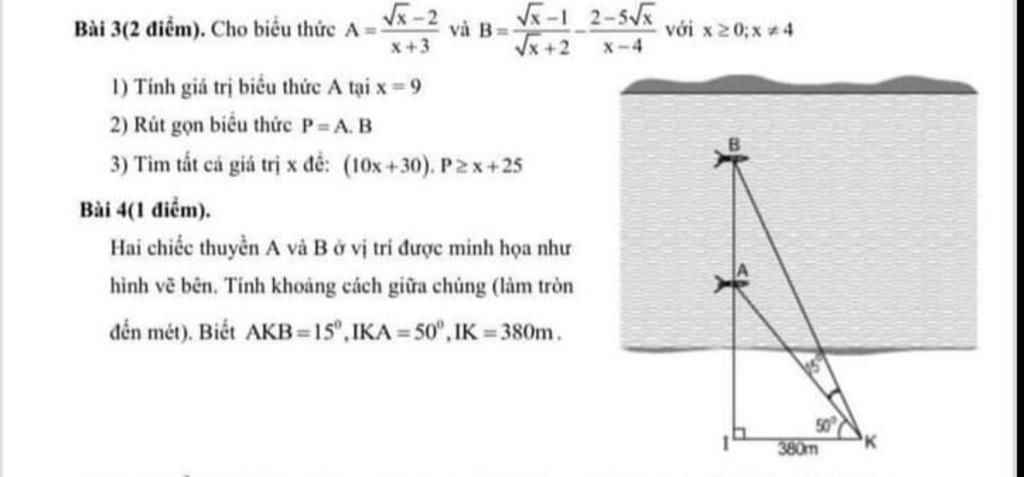
Làm hộ em phần tính các góc thôi ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
làm hộ em phần 3) thôi ạ mấy phần kia em đã làm đc r ạ
24 tháng 10 2021
\(P=A.B=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}.\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\)
\(=1+\dfrac{9}{\sqrt{x}-3}\le1+\dfrac{9}{0-3}=1-3=-2\)
\(maxP=-2\Leftrightarrow x=0\)
24 tháng 10 2021
\(1,x=16\Leftrightarrow A=\dfrac{4-1}{4-3}=\dfrac{3}{1}=3\\ 2,B=\dfrac{x+2\sqrt{x}-3+5\sqrt{x}+5+4}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{x+7\sqrt{x}+6}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ B=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+6\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\\ 3,P=AB=\dfrac{\sqrt{x}-1}{\sqrt{x}-3}\cdot\dfrac{\sqrt{x}+6}{\sqrt{x}-1}=\dfrac{\sqrt{x}+6}{\sqrt{x}-3}\\ P=1+\dfrac{9}{\sqrt{x}-3}\\ Vì.\sqrt{x}-3\ge-3\Leftrightarrow\dfrac{9}{\sqrt{x}-3}\le-3\\ \Leftrightarrow P=1+\dfrac{9}{\sqrt{x}-3}\le1-3=-2\\ P_{max}=-2\Leftrightarrow x=0\)
1 tháng 11 2021
Bài 3:
a: Thay x=9 vào A, ta được:
\(A=\dfrac{3-2}{3+3}=\dfrac{1}{6}\)
2 tháng 11 2021
Bài 3:
\(1,x=9\Leftrightarrow A=\dfrac{3-2}{9+3}=\dfrac{1}{12}\\ 2,P=AB=\dfrac{\sqrt{x}-2}{x+3}\cdot\dfrac{x-3\sqrt{x}+2-2+5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}+2\right)}{\left(x+3\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}}{x+3}\\ 3,\left(10x+30\right)P\ge x+25\\ \Leftrightarrow\dfrac{3\sqrt{x}\left(x+3\right)}{x+3}-x-25\ge0\\ \Leftrightarrow3\sqrt{x}-x-25\ge0\\ \Leftrightarrow-\left(x-3\sqrt{x}+\dfrac{9}{4}\right)-\dfrac{91}{4}\ge0\\ \Leftrightarrow-\left(\sqrt{x}-\dfrac{3}{2}\right)^2-\dfrac{91}{4}\ge0\left(vô.lí\right)\\ \Leftrightarrow x\in\varnothing\)
13 tháng 7 2021
1)
a) 4y2-4xy+x2= x2-4xy+4y2= (x-2y)2
b) 9x2-12xy+4y2= (3x)2-2.3x.2y+(2y)2= (3x-2y)2
c) 16x2-25=(4x)2-52= (4x-5)(4x+5)
d) 1-9y2= 12-(3y)2=(1-3y)(1+3y)
13 tháng 7 2021
g) x3-27y3= (x-3y)(x2+3xy+9y2)
h) 64 + 8x3=(4+2x)(16+8x+4x2)
6 tháng 12 2021
Bài 12:
a: Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
15 tháng 3 2022
a. \(\widehat{DAB}=\widehat{ABC}=\widehat{BCE}=90^0\)
\(\widehat{ABD}=180^0-\widehat{ABC}-\widehat{EBC}=180^0-60^0-\left(180^0-\widehat{BCE}-\widehat{CEB}\right)=180^0-60^0-\left(180^0-60-\widehat{CEB}\right)=\widehat{CEB}\)\(\Rightarrow\)△ABD∼△CEB (g-g).
\(\Rightarrow\dfrac{AD}{CB}=\dfrac{AB}{CE}\Rightarrow AD.CE=CB.AB\Rightarrow AD.CE=a^2\) không đổi
b. \(\widehat{CAD}=\widehat{BAD}+\widehat{BAC}=60^0+60^0=\widehat{BCE}+\widehat{ACB}=\widehat{ACE}\)
\(\dfrac{AD}{CB}=\dfrac{AB}{CE}\Rightarrow\dfrac{AD}{AC}=\dfrac{AC}{CE}\)
\(\Rightarrow\)△ACD∼△CEA (c-g-c)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ACD}=\widehat{CEA}\\\dfrac{CE}{AC}=\dfrac{EA}{CD}\end{matrix}\right.\)
\(\Rightarrow\)△ACK∼△AEC (g-g).
\(\Rightarrow\dfrac{CK}{EC}=\dfrac{AK}{AC}\Rightarrow\dfrac{CE}{AC}=\dfrac{CK}{AK}\)
\(\Rightarrow\dfrac{AE}{CD}=\dfrac{CK}{AK}\Rightarrow AE.AK=CD.CK\)