Viết các công thức tính vận tốc và quãng đường đi được của vật rơi tự do.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Công thức tính vận tốc của sự rơi tự do: v = gt
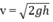
Công thức tính quãng đường đi được của sự rơi tự do: S = (1/2).g.t2

- Sự rơi tự do là sự rơi chỉ dưới tác dụng của trọng lực
- CT tính vận tốc: v = gt
- ______ quãng đường: \(s=\dfrac{1}{2}gt^2\)
- Sự rơi tự do là sự rơi chỉ dưới tác dụng của trọng lực
- CT tính vận tốc: v = gt
- ______ quãng đường: s=12gt2

Ta có:
\(\begin{array}{l}h'\left( 2 \right) = \mathop {\lim }\limits_{t \to 2} \frac{{h\left( t \right) - h\left( 2 \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{0,81{t^2} - 0,{{81.2}^2}}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{0,81\left( {{t^2} - {2^2}} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} \frac{{0,81\left( {t - 2} \right)\left( {t + 2} \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} 0,81\left( {t + 2} \right) = 0,81\left( {2 + 2} \right) = 3,24\end{array}\)
Vậy vận tốc tức thời của chuyển động lúc \(t = 2\) là: \(v\left( 2 \right) = h'\left( 2 \right) = 3,24\left( {m/s} \right)\)

Để giải bài toán này, ta sử dụng hai công thức sau:
Quãng đường chuyển động của vật rơi tự do: S = 5t²
Vận tốc của vật rơi tự do: V = 9,8t
Để tìm thời điểm vận động viên phải bật dù, ta cần tính thời gian mà vận động viên rơi từ độ cao 3970m đến cách mặt đất 845m:
Đầu tiên, ta tính quãng đường rơi của vận động viên: 3970 m - 845 m = 3125 m
Sau đó, ta sử dụng công thức quãng đường chuyển động của vật rơi tự do để tính thời gian rơi của vận động viên từ độ cao 3125m: S = 5t² 3125 = 5t² t² = 625 t = 25 giây
Vậy sau 25 giây từ lúc bắt đầu nhảy, vận động viên phải bật dù.
Để tính vận tốc rơi của vận động viên tại thời điểm cách mặt đất 845m, ta sử dụng công thức vận tốc của vật rơi tự do:
V = 9,8t
Ta thấy được rằng tại thời điểm cách mặt đất 845m, thời gian rơi của vận động viên là: S = 5t² 845 = 5t² t² = 169 t = 13 giây
Vậy sau 13 giây từ lúc bắt đầu nhảy, vận động viên cách mặt đất 845m và vận tốc rơi của vận động viên là: V = 9,8t = 9,8 x 13 = 127,4 (m/s)
Vậy sau 13 giây từ lúc bắt đầu nhảy, vận tốc rơi của vận động viên là 127,4 (m/s).

\(\Rightarrow\left\{{}\begin{matrix}t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2.125}{10}}=5s\\v=gt=10.5=50m/s\\h\left(3s\right)=\dfrac{1}{2}g.3^2=45m\\h\left(2s-cuối\right)=h-h\left(3s\right)=125-45=80m\end{matrix}\right.\)

a) Quãng đường vật rơi trong 2s đầu:
\(S=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot2^2=20m\)
b) Vận tốc vật rơi trong 5s đầu tiên: \(v=gt=10\cdot5=50\) m/s
c) Quãng đường vật đi được trong giây thứ 7:
\(S=\dfrac{1}{2}gt^2-\dfrac{1}{2}g\left(t-1\right)^2=\dfrac{1}{2}\cdot10\cdot7^2-\dfrac{1}{2}\cdot10\cdot6^2=65m\)


- Công thức tính vận tốc:
v = gt
trong đó, g là gia tốc của chuyển động rơi tự do, gọi tắt là gia tốc rơi tự do
- Công thức tính quãng đường đi được của vật rơi tự do:
s = 1/2 gt2
trong đó: s là quãng đường đi được, còn t là thời gian rơi.
- Công thức tính vận tốc:
v = gt
trong đó, g là gia tốc của chuyển động rơi tự do, gọi tắt là gia tốc rơi tự do
- Công thức tính quãng đường đi được của vật rơi tự do:
s = 1/2 gt2
trong đó: s là quãng đường đi được, còn t là thời gian rơi.