1) Cho hai hàm sô y =x^2 / 2 có đồ thị (P) và y= -x+m có đồ thi (Dm).Xác định giá trị của m để:
a) (Dm) cắt (P) tại điểm có hoành độ bằng 1
b) (Dm) cắt (P) tại 2 điểm phân biệt
c) (Dm) tiếp xúc (P). Xác định toạ độ giao điểm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
PT hoành độ giao điểm:
$x^2-(m-1)x-m-1=0(*)$
Để $(P)$ và $(dm)$ cắt nhau tại 1 điểm có tọa độ nguyên thì PT $(*)$ phải có nghiệm nguyên
Điều này xảy ra khi $\Delta=(m-1)^2+4(m+1)=a^2$ với $a$ là số tự nhiên
$\Leftrightarrow m^2+2m+5=a^2$
$\Leftrightarrow (m+1)^2+4=a^2$
$\Leftrightarrow 4=(a-m-1)(a+m+1)$
Vì $a+m+1>0$ và $a+m+1> a-m-1$ với mọi $a$ tự nhiên, $m$ nguyên dương nên:
$a+m+1=4; a-m-1=1$
$\Rightarrow m=\frac{1}{2}$ (vô lý)
Vậy không tồn tại $m$ thỏa mãn điều kiện đề bài.

a: Bạn bổ sung đề đi bạn
b: thay x=-3 và y=0 vào (d), ta được:
\(-3\left(2m+1\right)-m+3=0\)
=>-6m-3-m+3=0
=>-7m=0
=>m=0
d: y=(2m+1)x-m+3
=2mx+x-m+3
=m(2x-1)+x+3
Tọa độ điểm cố định mà (1) luôn đi qua là:
\(\left\{{}\begin{matrix}2x-1=0\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=3+\dfrac{1}{2}=\dfrac{7}{2}\end{matrix}\right.\)

a: Thay x=0 và y=2 vào (d), ta được:
a=2
b: Thay x=-1 và y=0 vào (d), ta được:
\(-\left(a-2\right)+a=0\)
\(\Leftrightarrow2=0\)(vô lý)

a: Thay x=0 và y=2 vào (d), ta được:
\(0\left(m-1\right)+m=2\)
=>m+0=2
=>m=2
b: Thay x=-3 vào y=0 vào (d), ta được:
\(-3\left(m-1\right)+m=0\)
=>-3m+3+m=0
=>-2m+3=0
=>-2m=-3
=>\(m=\dfrac{3}{2}\)
c: Khi m=2 thì (d): \(y=\left(2-1\right)x+2=x+2\)
Khi m=3/2 thì (d): \(y=\left(\dfrac{3}{2}-1\right)x+\dfrac{3}{2}=\dfrac{1}{2}x+\dfrac{3}{2}\)
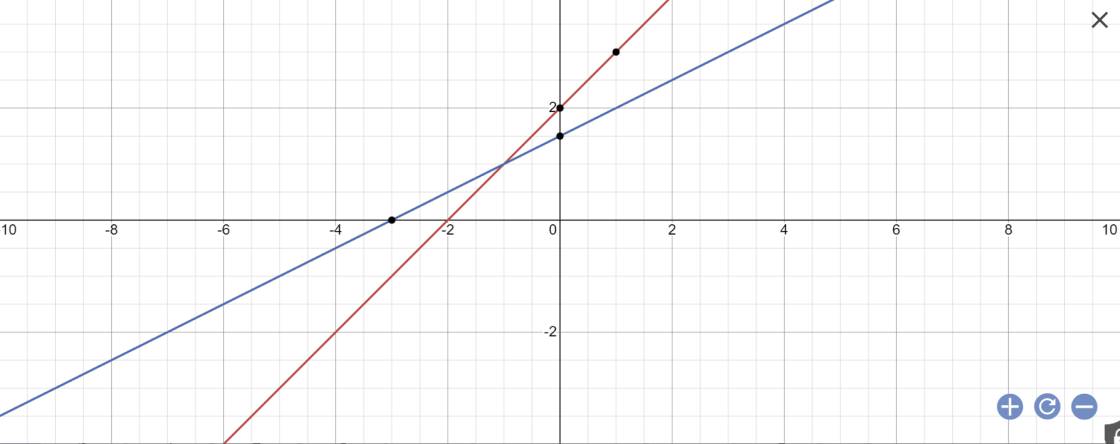
Tọa độ giao điểm của hai đường thẳng này là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}x+2=\dfrac{1}{2}x+\dfrac{3}{2}\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x-\dfrac{1}{2}x=\dfrac{3}{2}-2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{1}{2}x=-\dfrac{1}{2}\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-1+2=1\end{matrix}\right.\)
a: Thay x=1 vào (P), ta được:
\(y=\dfrac{1^2}{2}=\dfrac{1}{2}\)
Thay x=1 và y=1/2 vào y=m-x, ta được:
m-1=1/2
hay m=3/2
b: Phương trình hoành độ giao điểm là:
\(\dfrac{1}{2}x^2+x-m=0\)
\(\text{Δ}=1^2-4\cdot\dfrac{1}{2}\cdot\left(-m\right)=2m+1\)
Để (P) cắt (d) tại hai điểm phân biệt thì 2m+1>0
hay m>-1/2
c: Để (P) tiếp xúc với (d) thì 2m+1=0
hay m=-1/2